Chapitre 7 Régression logistique

7.1 Généralités

Il existe aussi plusieurs procédures dans R permettant d’effectuer une régression logistique. Nous travaillerons principalement avec la fonction glm() qui comblera la plupart de vos besoins de ce côté. Notez que nous utiliserons cette même fonction pour d’autres types de modèles que nous verrons plus tard (e.g., Poisson, binomiale négative). Puisque la fonction glm() peut être utilisée pour plusieurs types de régression, il faudra donc indiquer la famille de régression qui nous intéresse, dans ce cas-ci l’argument family=binomial indiquera que notre variable dépendante est binomiale (i.e., elle prend seulement 2 valeurs, par exemple 0 ou 1). Dans ce cas, la fonction de lien par défaut sera la fonction logit. On aura donc une régression logistique. Notez qu’à part l’ajout de family=binomial la syntaxe est identique à celle de la fonction lm().

Le jeu de donnée Nocardia sera utilisé pour cette section.

#Nous importons le jeu de données
nocardia <-read.csv(file="nocardia.csv", 
                    header=TRUE, 
                    sep=";")
head(nocardia)
##   id casecont numcow prod        bscc dbarn dout dcprep dcpct dneo dclox doth
## 1  1        0     16 20,1 446,2000122     2    1      4     0    0     0    1
## 2  2        0     16 22,3         214     2    1      3   100    1     0    1
## 3  3        0     18 24,9         260     2    1      3    25    0     0    1
## 4  4        0     18      184,1999969     1    1      3     1    0     0    1
## 5  5        0     20 34,5 61,40000153     2    1      3   100    0     1    0
## 6  6        0     21 22,7 80,19999695     1    1      3     0    0     0    0
#Nous indiquons les variables catégoriques dans le jeu de données
nocardia$dbarn <- factor(nocardia$dbarn) 
nocardia$dneo <- factor(nocardia$dneo) 
nocardia$dclox <- factor(nocardia$dclox) 

#Nous faisons une régression logistique

modele_1 <- glm(data = nocardia, 
                casecont ~ dcpct + dbarn, 
                family = binomial
                )
summary(modele_1)
## 
## Call:
## glm(formula = casecont ~ dcpct + dbarn, family = binomial, data = nocardia)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.5537  -1.2441   0.1261   1.1063   1.9280  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)   
## (Intercept) -1.025831   0.634461  -1.617  0.10591   
## dcpct        0.018774   0.006196   3.030  0.00244 **
## dbarn2      -0.681944   0.449586  -1.517  0.12931   
## dbarn3       0.038615   0.960075   0.040  0.96792   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 149.72  on 107  degrees of freedom
## Residual deviance: 135.49  on 104  degrees of freedom
## AIC: 143.49
## 
## Number of Fisher Scoring iterations: 4

Plusieurs éléments sont présentés. D’abord, des résultats sur les résiduels de déviance (on y reviendra). Puis les coefficients, erreur-types et les résultats des tests de Wald qui permettent de tester chacun des coefficients, un à la fois (l’hypothèse nulle est que ce β=0). Notez que le résultat “Residual deviance” (135.49 avec 104 degrés de liberté) correspond au -2 log likelihood.

7.2 Effectuer un test de rapport de vraisemblance

Pour comparer le modèle complet avec le modèle nul (i.e., le modèle avec seulement un intercept) il faudra faire un test de rapport de vraisemblance (likelihood ratio test). La fonction lrtest() du package lmtest permet de réaliser ce genre de test.

library(lmtest)
lrtest(modele_1) #Raélise un test de rapport de vraisemblance du modèle
## Likelihood ratio test
## 
## Model 1: casecont ~ dcpct + dbarn
## Model 2: casecont ~ 1
##   #Df  LogLik Df  Chisq Pr(>Chisq)   
## 1   4 -67.747                        
## 2   1 -74.860 -3 14.225   0.002614 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Nous voyons bien les deux modèles qui sont comparés. Ici, la conclusion serait qu’au moins un des coefficients (dcpct ou dbarn) est différent de 0 (P=0.003).

Pour comparer un modèle complet vs. un modèle réduit, on utilisera la même fonction du même package, mais après avoir créé les deux modèles.

mod_red<-glm(data=nocardia, 
             casecont~ dcpct + dbarn, 
             family="binomial" 
             )

mod_comp<-glm(data=nocardia, 
              casecont~ dcpct + dneo + dclox + dbarn, 
              family="binomial" 
              )

lrtest(mod_comp, mod_red) #likelihood ratio test
## Likelihood ratio test
## 
## Model 1: casecont ~ dcpct + dneo + dclox + dbarn
## Model 2: casecont ~ dcpct + dbarn
##   #Df  LogLik Df  Chisq Pr(>Chisq)    
## 1   6 -51.158                         
## 2   4 -67.747 -2 33.178  6.244e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La conclusion serait qu’au moins un des deux coefficients (dneo et/ou dclox) est différent de 0 (P<0.001). C’est aussi à l’aide de la fonction lrtest qu’on pourra réaliser un test sur l’ensemble des variables indicatrices d’une variables avec > 2 catégories, l’équivalent du test de F en régression linéaire.

7.3 Ajouter des IC95

Vous pouvez ajouter des IC95 avec la fonction confint(), comme vu précédemment.

confint(modele_1, 
        level= 0.95)
##                    2.5 %     97.5 %
## (Intercept) -2.354149597 0.16936727
## dcpct        0.007243426 0.03183774
## dbarn2      -1.582513404 0.19021182
## dbarn3      -1.882433338 2.00161262

7.4 Choisir valeur de référence pour les variables catégoriques

Vous pouvez choisir les valeurs de référence pour les variables catégoriques avec la fonction relevel(), comme vu précédemment.

nocardia <- within(nocardia, 
                   dbarn<-relevel(dbarn, 
                                  ref=1)
                   ) #Dans ce cas, ça ne changera rien puisque R avait déjà pris la valeur 1 comme catégorie de référence

7.5 Produire des tables de résultats

Le package jtools vous permet de présenter des tables de résultats plus jolies:

library(jtools)
j <- summ(modele_1, 
          confint = TRUE)
j$coeftable
##                    Est.         2.5%      97.5%      z val.           p
## (Intercept) -1.02583119 -2.269351164 0.21768878 -1.61685557 0.105909460
## dcpct        0.01877361  0.006630146 0.03091708  3.03007440 0.002444935
## dbarn2      -0.68194417 -1.563115697 0.19922736 -1.51682840 0.129310014
## dbarn3       0.03861550 -1.843097887 1.92032888  0.04022131 0.967916686

Ou encore, si vous utilisez RMarkdown.

library(knitr)
library(kableExtra)
kable(round(j$coeftable, 
            digits=3), 
      caption="Résultats du modèle."
      )%>%
  kable_styling()
Table 7.1: Résultats du modèle.
Est. 2.5% 97.5% z val. p
(Intercept) -1.026 -2.269 0.218 -1.617 0.106
dcpct 0.019 0.007 0.031 3.030 0.002
dbarn2 -0.682 -1.563 0.199 -1.517 0.129
dbarn3 0.039 -1.843 1.920 0.040 0.968

7.5.1 Présenter les rapports de cotes plutôt que les log odds

Si vous désirez obtenir les rapports de cotes, alors vous pouvez simplement demander l’exposant de vos résultats comme ceci.

#Nous demandons de présenter les coefficients du modèle mis à l'exposant
exp(coef(modele_1))
## (Intercept)       dcpct      dbarn2      dbarn3 
##   0.3584984   1.0189509   0.5056330   1.0393708

Pour obtenir rapports de cotes et IC95 des rapports de cotes:

#Ici nous avons demandé de créer une colonne représentant un vecteur de nombres (que nous avons nommé OR et qui seront les OR) et d'y juxtaposer (fonction cbind) les IC95 du modèle. Il ne reste plus qu'à mettre en exposant les valeurs contenues dans ces 3 colonnes pour avoir des OR et leurs IC95
exp(cbind(OR = coef(modele_1), 
          confint(modele_1)
          )
    )
##                    OR      2.5 %   97.5 %
## (Intercept) 0.3584984 0.09497424 1.184555
## dcpct       1.0189509 1.00726972 1.032350
## dbarn2      0.5056330 0.20545805 1.209506
## dbarn3      1.0393708 0.15221925 7.400981

On pourrait même arrondir, pour faire plus joli, et produire la table avec RMarkdown.

library(knitr)
library(kableExtra)
kable(round(exp(cbind(OR = coef(modele_1), 
                      confint(modele_1)
                      )
                ), 
            digits=2), 
      caption="Résultats du modèle."
      )%>%
  kable_styling()
Table 7.2: Résultats du modèle.
OR 2.5 % 97.5 %
(Intercept) 0.36 0.09 1.18
dcpct 1.02 1.01 1.03
dbarn2 0.51 0.21 1.21
dbarn3 1.04 0.15 7.40

Dans ce cas, on voit qu’une augmentation de 1 unité de dcpct (le % de vaches traitées au tarissement) augmente les odds de mammite à nocardia par un facteur de 1.02 (IC95: 1.01, 1.03).

7.6 Spécifier pour quelle augmentation d’un prédicteur continu le rapport de cotes est calculé

Si vous voulez produire le rapport de cotes pour une augmentation de 10 ou 20 unités de dcpct vous pourriez mettre à l’échelle la variable dcpct afin que celle-ci représente une augmentation de 10 ou 20 unités et utiliser ces nouvelles variables dans le modèle. Par exemple, pour une augmentation de 10 points de pourcentage:

nocardia$dcpct10 <- nocardia$dcpct/10

modele_10 <- glm(data = nocardia, 
                 casecont ~ dcpct10 + dbarn, 
                 family = binomial
                 )

round(exp(cbind(OR = coef(modele_10),
                confint(modele_10)
                )
          ), 
      digits=2)
##               OR 2.5 % 97.5 %
## (Intercept) 0.36  0.09   1.18
## dcpct10     1.21  1.08   1.37
## dbarn2      0.51  0.21   1.21
## dbarn3      1.04  0.15   7.40

Donc une augmentation de 10 unités multiplie les odds de nocardia par 1.21 (IC95: 1.08, 1.37).

Vous auriez aussi pu simplement multiplier le coefficient et ses erreur-types par 10 et ensuite les mettre à l’exposant:

#Créons un objet avec les résultats du modèle
library(jtools)
res <- summ(modele_1)

#Dans l'objet res$coeftable la première colonne est pour les coefficents et la 2ième est pour les erreur-types. Et la 2ième rangée est pour dcpct. Le coefficient de dcpct est donc en rangée 2 et colone 1 ou res$coeftable[2,1]
OR <- exp(10*res$coeftable[2,1])

#Et les erreur-types sont en res$coeftable[2,2]
L95 <- exp(10*res$coeftable[2,1]-1.96*10*res$coeftable[2,2])
U95 <- exp(10*res$coeftable[2,1]+1.96*10*res$coeftable[2,2])

#De là:
round(cbind(OR10=OR, 
            LowerCI=L95, 
            UpperCI=U95), 
      digits=2)
##      OR10 LowerCI UpperCI
## [1,] 1.21    1.07    1.36

Comme vous le voyez, il y a plusieurs manières d’arriver au même résultat!

7.7 Évaluer une interaction entre 2 variables

Comme pour la fonction lm() vous n’avez qu’à indiquer dans votre modèle la multiplication des effets (dneo*dclox). La fonction glm() se chargera alors de créer toutes les variables indicatrices nécessaires.

modele_inter <- glm(data = nocardia, 
                    casecont ~ dcpct + dneo*dclox, 
                    family = binomial
                    )
library(jtools)
inter <- summ(modele_inter, 
              confint = TRUE)
inter$coeftable
##                     Est.         2.5%       97.5%    z val.            p
## (Intercept)  -3.77689649 -5.723632083 -1.83016091 -3.802561 0.0001432079
## dcpct         0.02261751  0.007480181  0.03775484  2.928489 0.0034061354
## dneo1         3.18400225  1.543122188  4.82488232  3.803160 0.0001428619
## dclox1        0.44570471 -1.565269702  2.45667913  0.434399 0.6639987570
## dneo1:dclox1 -2.55199707 -4.913900617 -0.19009352 -2.117708 0.0341997943

7.8 Comparer rapports de cotes pour une combinaison spécifique de prédicteurs

La fonction pairs() du package emmeans vous permet de comparer toutes les combinaisons possibles d’un ou plusieurs prédicteurs catégoriques et/ou quantitatifs.

library(emmeans)
contrast <- emmeans(modele_inter, 
                    c("dneo", "dclox")
                    ) 
pairs(contrast)  
##  contrast                    estimate    SE  df z.ratio p.value
##  dneo0 dclox0 - dneo1 dclox0   -3.184 0.837 Inf  -3.803  0.0008
##  dneo0 dclox0 - dneo0 dclox1   -0.446 1.026 Inf  -0.434  0.9726
##  dneo0 dclox0 - dneo1 dclox1   -1.078 0.953 Inf  -1.131  0.6705
##  dneo1 dclox0 - dneo0 dclox1    2.738 0.773 Inf   3.541  0.0023
##  dneo1 dclox0 - dneo1 dclox1    2.106 0.666 Inf   3.164  0.0085
##  dneo0 dclox1 - dneo1 dclox1   -0.632 0.873 Inf  -0.724  0.8875
## 
## Results are given on the log odds ratio (not the response) scale. 
## P value adjustment: tukey method for comparing a family of 4 estimates

Rappelez-vous, si vous utilisez la fonction confint()sur votre fonction pairs(), vous aurez alors aussi les IC95.

library(emmeans)
contrast <- emmeans(modele_inter, 
                    c("dneo", "dclox")
                    ) 
confint(pairs(contrast))  
##  contrast                    estimate    SE  df asymp.LCL asymp.UCL
##  dneo0 dclox0 - dneo1 dclox0   -3.184 0.837 Inf    -5.335     -1.03
##  dneo0 dclox0 - dneo0 dclox1   -0.446 1.026 Inf    -3.082      2.19
##  dneo0 dclox0 - dneo1 dclox1   -1.078 0.953 Inf    -3.526      1.37
##  dneo1 dclox0 - dneo0 dclox1    2.738 0.773 Inf     0.752      4.73
##  dneo1 dclox0 - dneo1 dclox1    2.106 0.666 Inf     0.396      3.82
##  dneo0 dclox1 - dneo1 dclox1   -0.632 0.873 Inf    -2.874      1.61
## 
## Results are given on the log odds ratio (not the response) scale. 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 4 estimates

Nous avons maintenant tous les contrastes pour les différentes combinaisons de dneo et dclox. Par exemple, la première ligne compare ceux qui n’utilisaient aucun des deux produits (dneo0 et dclox0) vs. ceux qui utilisait dneo mais pas dclox (dneo1 et dclox0).

De là, si on voulait avoir les rapports de cotes pour les différentes comparaisons plutôt que les log odds, nous pourrions ajouter l’argument type="response".

confint(pairs(contrast, 
              type="response")
        )
##  contrast                    odds.ratio      SE  df asymp.LCL asymp.UCL
##  dneo0 dclox0 / dneo1 dclox0     0.0414  0.0347 Inf   0.00482     0.356
##  dneo0 dclox0 / dneo0 dclox1     0.6404  0.6570 Inf   0.04589     8.937
##  dneo0 dclox0 / dneo1 dclox1     0.3404  0.3244 Inf   0.02942     3.939
##  dneo1 dclox0 / dneo0 dclox1    15.4606 11.9565 Inf   2.12025   112.737
##  dneo1 dclox0 / dneo1 dclox1     8.2177  5.4711 Inf   1.48575    45.452
##  dneo0 dclox1 / dneo1 dclox1     0.5315  0.4639 Inf   0.05646     5.004
## 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 4 estimates 
## Intervals are back-transformed from the log odds ratio scale

Dans ce cas, les odds de nocardia étaient 15.5 (95CI: 2.1, 112.7) fois plus grandes pour les troupeaux utilisant seulement neomycine (1 et 0) vs. ceux utilisant seulement la cloxacilline (0 et 1).

7.9 Présenter l’effet des prédicteurs sur une échelle de probabilité

Présenter vos résultats sur une échelle de probabilité (plutôt que odds ou log odds) permettra de mieux illustrer l’effet de vos différents prédicteurs. La fonction plot_model() du package sjPlotvous permet d’obtenir une telle représentation graphique de vos résultats. L’option type="eff" permet de rapporter les résultats sur l’échelle d’une probabilité (plutôt que odds, log odds ou OR).

library(sjPlot)
plot_model(modele_inter, 
           type="eff")
## $dcpct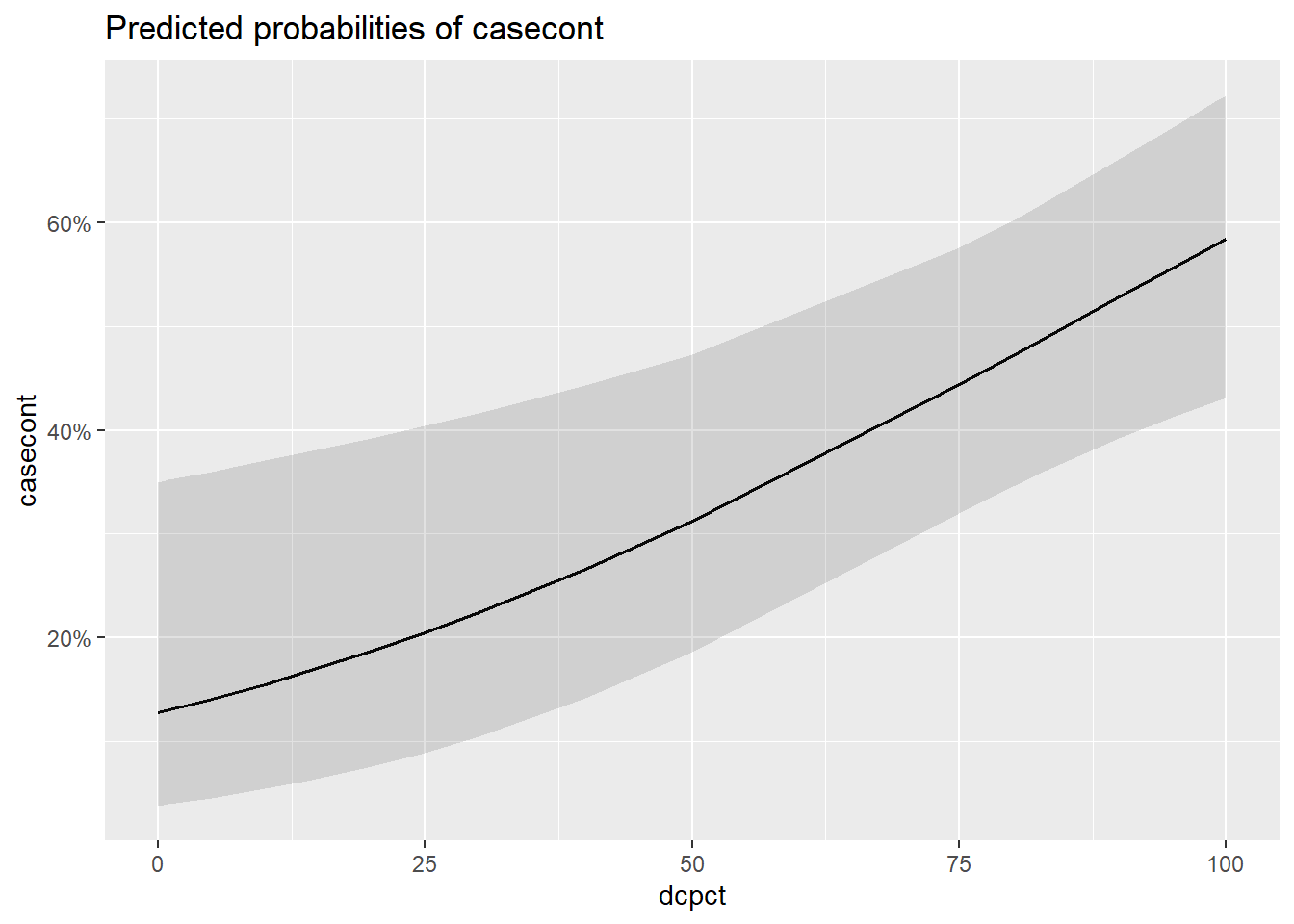
Effet de différentes variables sur la probabilité de nocardia.

Figure 7.1: Effet de différentes variables sur la probabilité de nocardia. 

## 
## $dneo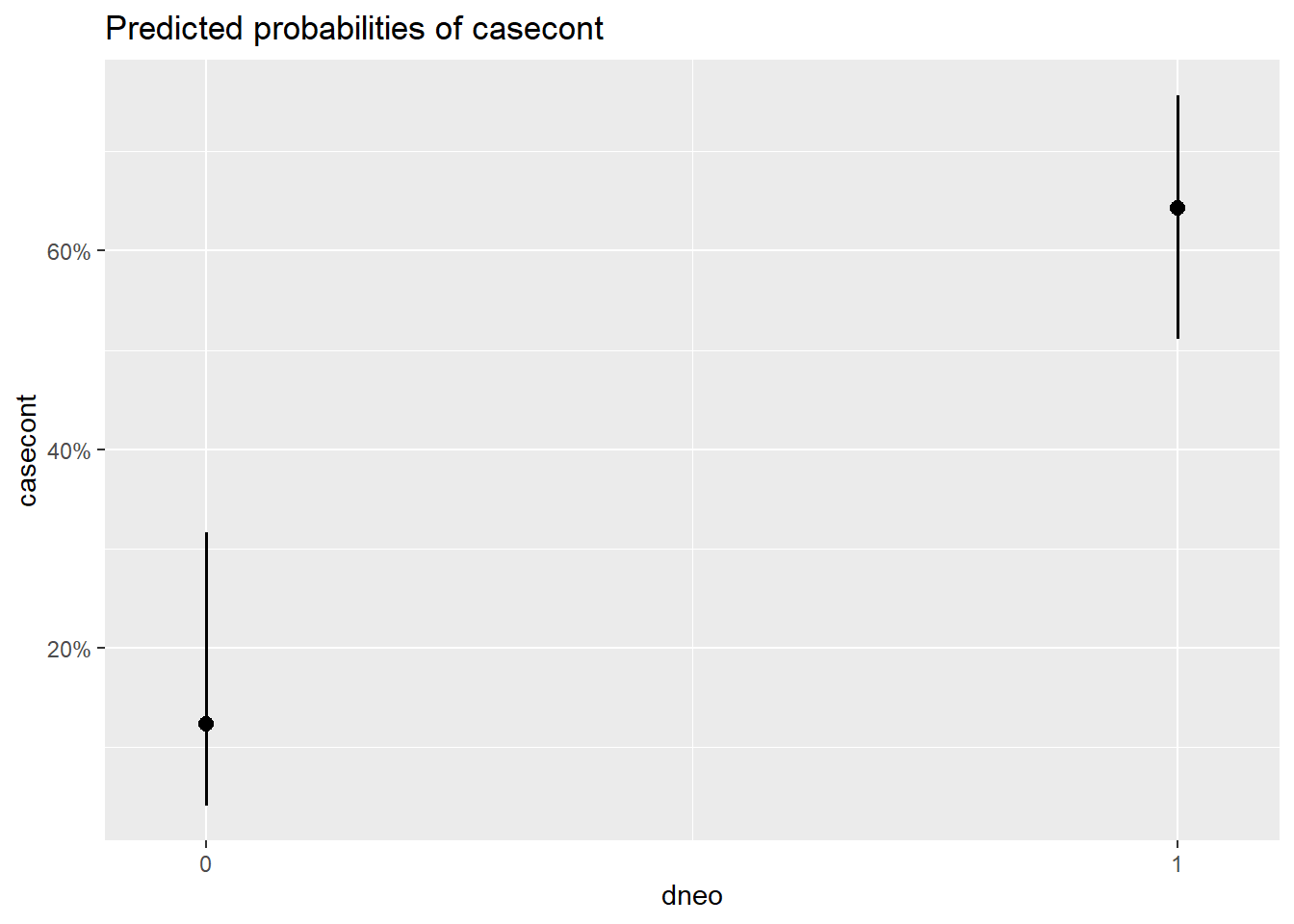
Effet de différentes variables sur la probabilité de nocardia.

Figure 7.2: Effet de différentes variables sur la probabilité de nocardia. 

## 
## $dclox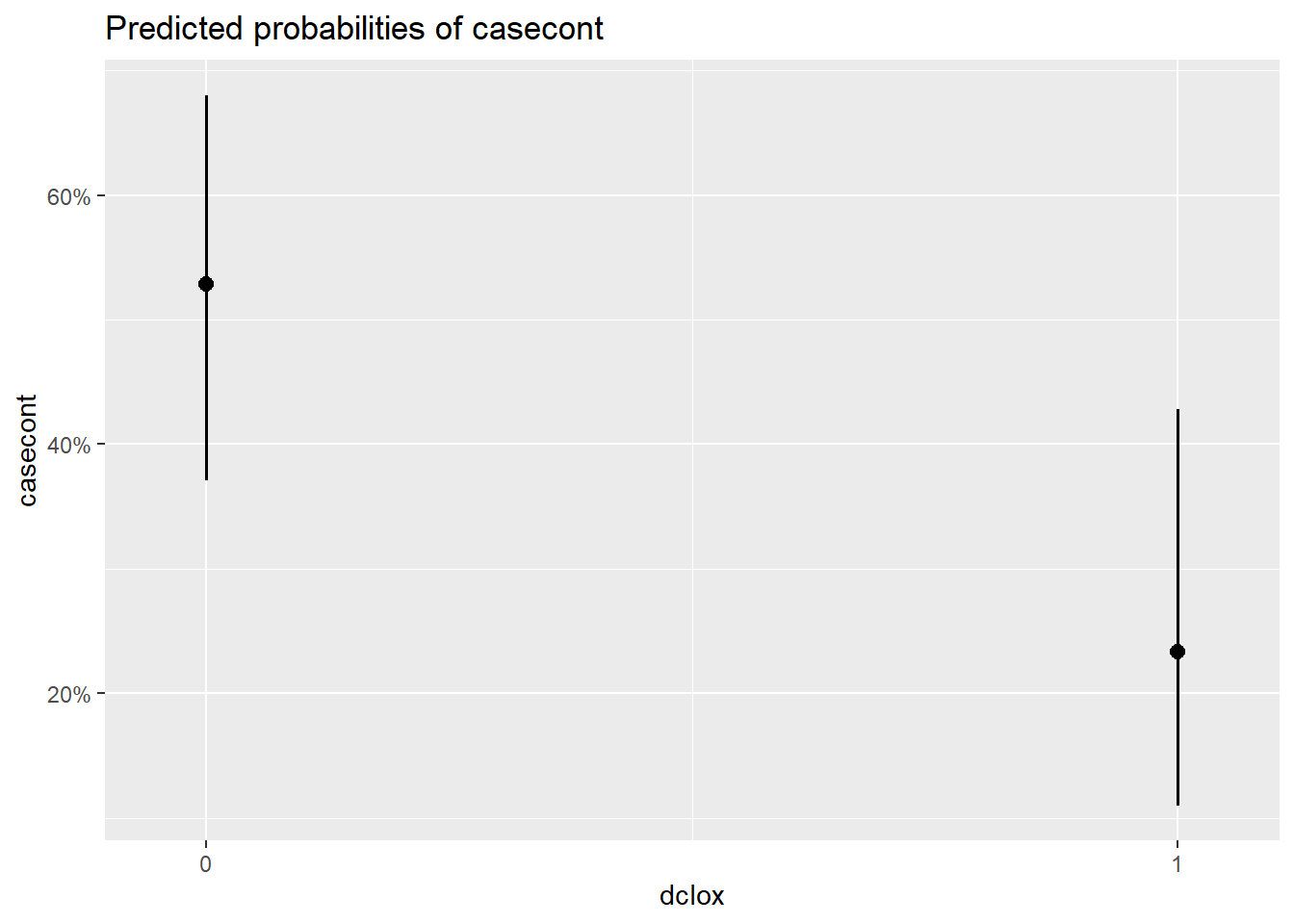
Effet de différentes variables sur la probabilité de nocardia.

Figure 7.3: Effet de différentes variables sur la probabilité de nocardia.

On voit alors les graphiques pour chacune des variables du modèle. Par contre, souvent on voudra voir tout ensemble dans un seul graphique. On peut alors ajouter l’argument terms=c("var1", "var2", "var3"). La première variable apparaitra en x, la deuxième en y et la troisième séparera la figure en 2 figures.

library(sjPlot)
plot_model(modele_inter, 
           type="eff", 
           terms=c("dcpct", "dneo", "dclox")
           )
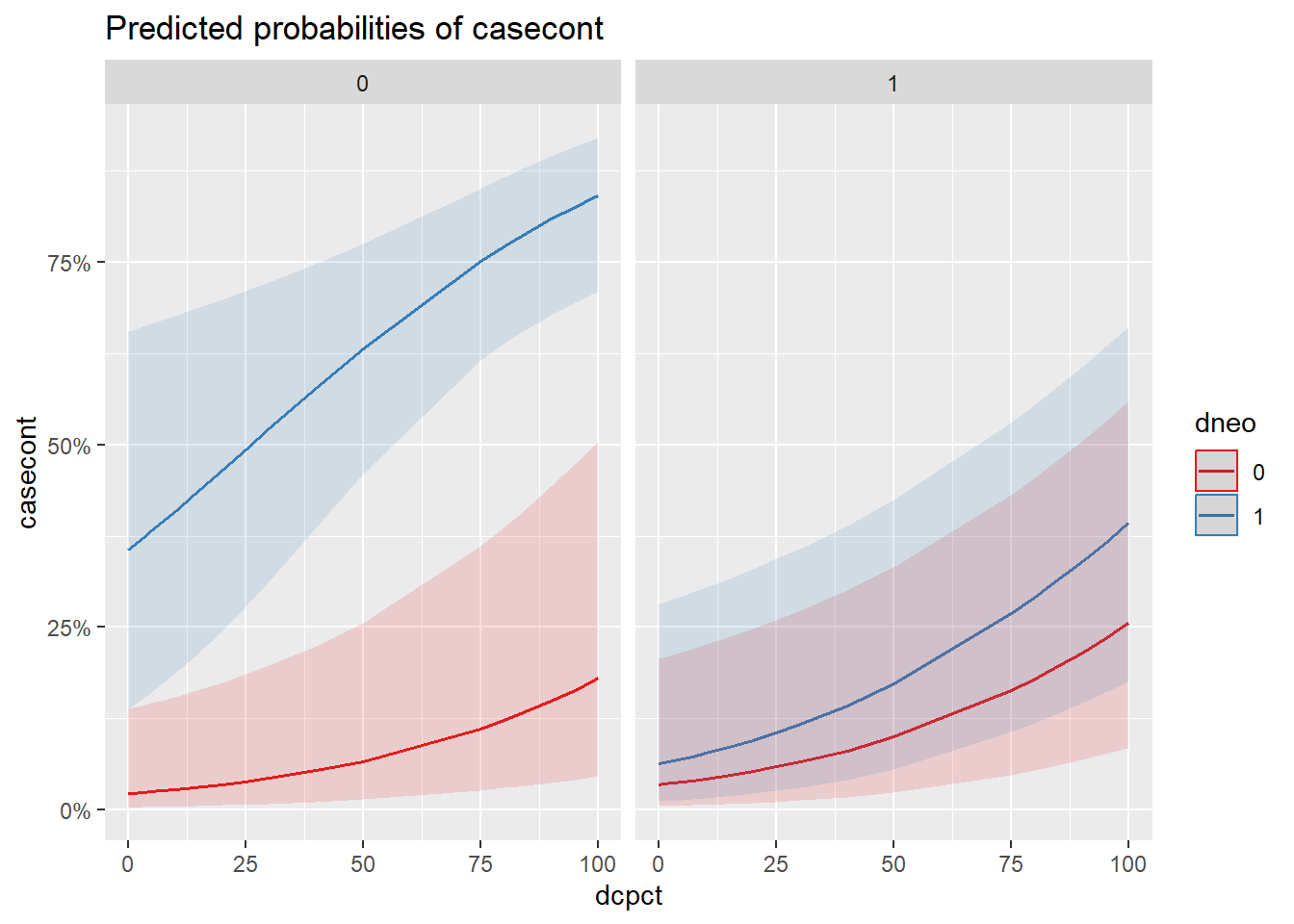
Effet de l'utilisation de la neomycine et du % de vache traitées au tarissement par niveau d'utilisation de la cloxacilline.

Figure 7.4: Effet de l’utilisation de la neomycine et du % de vache traitées au tarissement par niveau d’utilisation de la cloxacilline.

7.10 Linéarité de la relation (pour prédicteur quantitatif)

La linéarité de la relation est une supposition importante du modèle. Dans le modèle logistique, la relation entre le prédicteur et le log odds doit être une ligne droite, ce qui complique l’évaluation. Pour les prédicteurs quantitatifs, vous devrez toujours vérifier si cette supposition est bien respectée. Vous pouvez le faire, comme en régression linéaire, à l’aide du modèle polynomial (en ajoutant le \(prédicteur^2\) ou le \(prédicteur^2\) et le \(prédicteur^3\) dans votre modèle). Si les coefficients de ces termes sont significativement différents de zéro (i.e. P < 0.05), ont concluera que la relation est une courbe, ou une courbe avec un ou plusieurs points d’inflexion, respectivement.

7.11 Test de ‘fit’ de Hosmer-Lemeshow et de Pearson

La fonction hoslem.test() du package ResourceSelection permet de réaliser le test de Hosmer-Lemeshow. Il faut simplement indiquer l’objet “modèle” avec lequel vous voulez travailler (par exemple, ici modele_inter). Dans cet objet, il y a toujours une variable nommée \(y\) et hoslem.test() voudra l’utiliser, vous n’avez donc pas à modifier y dans le code plus bas. Il s’agit en fait de la variable réponse. Ont indique ensuite d’utiliser les valeurs prédites (fitted) et, encore une fois, l’objet “modèle” où elles se trouvent. Finalement on peut ou non indiquer le nombre de groupes utilisés pour le test, ici g=8.

library(ResourceSelection)
hoslem.test(modele_inter$y, 
            fitted(modele_inter),
            g=8
            )
## 
##  Hosmer and Lemeshow goodness of fit (GOF) test
## 
## data:  modele_inter$y, fitted(modele_inter)
## X-squared = 1.4887, df = 6, p-value = 0.9602

Dans ce cas, le test ne rejette pas l’hypothèse nulle (i.e. le modèle « fit » bien les données).

C’est beaucoup plus demandant de réaliser les tests de fit de Déviance ou de Pearson dans R. Si vous trouvez une manière simple de le faire, indiquez-le-nous! En théorie, ont peut générer les résiduels avec la fonction augment() du package broom. Puis, la fonction distinct() (du package dplyr) pourrait être utilisée pour ne conserver que les profils uniques de prédicteurs pour un jeu de données. La fonction dim() permettra de rapporter le nombre de lignes dans ce jeu de données réduit (i.e., le nombre de profils). Ensuite, ont pourrait faire la somme des résiduels de Pearson de chacun de ces profils après les avoir mis au carré avec la fonction sum() et l’argment ^2. La fonction length() permettra de calculer le nombre de coefficients dans le modèle. Puis, finalement, on cherche la probabilité d’observer cette valeur dans une table de chi-carré avec le nombre de degrés de liberté approprié (i.e., le nombre de profils unique - le nombre de coefficients) en utilisant la fonction pchisqr(). Ouf! Nous vous épargnons les détails…

7.12 Évaluation des profils extrêmes et/ou influents

Comme pour la fonction lm(), vous pouvez demander de créer une nouvelle table contenant, en plus de vos variables originales, les différentes valeurs (e.g. résiduels de Pearson, de déviance, probabilité prédite, leviers, Delta-Beta) qui serviront à évaluer votre modèle. La fonction augment() du package broom vous permet de le faire. Vous pourrez ensuite trier cette table pour identifier, par exemple, les observations avec les résiduels, leviers ou distance de Cook les plus extrêmes et essayer de comprendre si ces observations ont quelque chose en commun.

library(broom)
diag <- augment(modele_inter) #Nous venons de créer une nouvelle table dans laquelle les résiduels, distance de cook, etc se trouvent maintenant
head(diag)
## # A tibble: 6 × 10
##   casecont dcpct dneo  dclox .fitted .resid .std.resid   .hat .sigma  .cooksd
##      <int> <int> <fct> <fct>   <dbl>  <dbl>      <dbl>  <dbl>  <dbl>    <dbl>
## 1        0     0 0     0       -3.78 -0.213     -0.215 0.0216  1.01  0.000103
## 2        0   100 1     0        1.67 -1.92      -1.94  0.0209  0.988 0.0232  
## 3        0    25 0     0       -3.21 -0.281     -0.285 0.0291  1.01  0.000248
## 4        0     1 0     0       -3.75 -0.215     -0.218 0.0218  1.01  0.000107
## 5        0   100 0     1       -1.07 -0.768     -0.803 0.0847  1.00  0.00694 
## 6        0     0 0     0       -3.78 -0.213     -0.215 0.0216  1.01  0.000103

Notez que les valeurs prédites sont sur une échelle de log odds. Les valeurs prédites sur une échelle de probabilité ont cependant été conservées dans votre objet modèle. Vous pouvez donc simplement les ajouter à votre table de diagnostic, si vous le désirez.

diag$pred_prob <- modele_inter$fitted.values
head(diag)
## # A tibble: 6 × 11
##   casec…¹ dcpct dneo  dclox .fitted .resid .std.…²   .hat .sigma .cooksd pred_…³
##     <int> <int> <fct> <fct>   <dbl>  <dbl>   <dbl>  <dbl>  <dbl>   <dbl>   <dbl>
## 1       0     0 0     0       -3.78 -0.213  -0.215 0.0216  1.01  1.03e-4  0.0224
## 2       0   100 1     0        1.67 -1.92   -1.94  0.0209  0.988 2.32e-2  0.841 
## 3       0    25 0     0       -3.21 -0.281  -0.285 0.0291  1.01  2.48e-4  0.0387
## 4       0     1 0     0       -3.75 -0.215  -0.218 0.0218  1.01  1.07e-4  0.0229
## 5       0   100 0     1       -1.07 -0.768  -0.803 0.0847  1.00  6.94e-3  0.256 
## 6       0     0 0     0       -3.78 -0.213  -0.215 0.0216  1.01  1.03e-4  0.0224
## # … with abbreviated variable names ¹​casecont, ²​.std.resid, ³​pred_prob

La table suivante est un extrait des 10 premières observations de cette nouvelle table lorsque classée des résiduels de Pearson les plus grands aux plus petits. À partir de cette table, vous pourriez produire les graphiques qui vous intéresseront à l’aide de la fonction ggplot().

#Nous pouvons maintenant ordonner cette table pour voir les 10 observations avec les résiduels les plus larges
diag_res <- diag[order(-diag$.resid),]
head(diag_res, 10)
## # A tibble: 10 × 11
##    casecont dcpct dneo  dclox .fitted .resid .std.resid   .hat .sigma .cooksd
##       <int> <int> <fct> <fct>   <dbl>  <dbl>      <dbl>  <dbl>  <dbl>   <dbl>
##  1        1    10 0     0      -3.55    2.68       2.71 0.0243  0.971  0.178 
##  2        1    50 1     1      -1.57    1.87       1.93 0.0592  0.989  0.0641
##  3        1   100 0     0      -1.52    1.85       1.94 0.0901  0.988  0.0990
##  4        1    83 0     1      -1.45    1.82       1.89 0.0707  0.989  0.0700
##  5        1   100 0     1      -1.07    1.65       1.73 0.0847  0.992  0.0589
##  6        1   100 0     1      -1.07    1.65       1.73 0.0847  0.992  0.0589
##  7        1     1 1     0      -0.570   1.43       1.50 0.0893  0.996  0.0381
##  8        1   100 1     1      -0.437   1.37       1.42 0.0757  0.997  0.0275
##  9        1   100 1     1      -0.437   1.37       1.42 0.0757  0.997  0.0275
## 10        1   100 1     1      -0.437   1.37       1.42 0.0757  0.997  0.0275
## # … with 1 more variable: pred_prob <dbl>

Notez qu’une valeur prédite et un résiduel sont calculés pour chaque profil de prédicteur (et non pour chaque observation). Il est donc normal que les observations avec un profil de prédicteurs identique aient exactement les mêmes valeurs prédites et résiduels (e.g. les lignes 8, 9 et 10).

7.13 Sensibilité, spécificité et courbe ROC

La fonction roc() de la librairie pROC permet de créer un nouvel objet dans lequel la sensibilité (Se) et la spécificité (Sp) sont rapportés pour tous les seuils possibles de probabilité prédite par le modèle. Pour ce, vous devrez utiliser une table dans laquelle les valeurs prédites par le modèle sont rapportées (par exemple le jeu de données créé avec la fonction augment() de la librairie broom.

#Valeur prédictive du modèle
library(pROC)
roc_data <- roc(data=diag, 
                response="casecont", 
                predictor="pred_prob"
                )

#Présenter les sensibilités et spécificités des différents seuils dans une même table.
accu <- as.data.frame(round(cbind(Seuil=roc_data$thresholds, 
                    Se=roc_data$sensitivities, 
                    Sp=roc_data$specificities), 
              digits=2))

#Voir la table
library(knitr)
library(kableExtra)
kable(accu,  
      caption="Sensibilité et spécificité du modèle pour différents seuils de probabilité prédite.")%>%
  kable_styling()
Table 7.3: Sensibilité et spécificité du modèle pour différents seuils de probabilité prédite.
Seuil Se Sp
-Inf 1.00 0.00
0.02 1.00 0.13
0.02 1.00 0.15
0.03 1.00 0.17
0.03 0.98 0.17
0.04 0.98 0.19
0.05 0.98 0.20
0.09 0.98 0.22
0.14 0.98 0.24
0.17 0.96 0.26
0.18 0.96 0.28
0.18 0.94 0.41
0.22 0.93 0.41
0.27 0.89 0.57
0.32 0.89 0.59
0.35 0.89 0.61
0.37 0.87 0.61
0.38 0.87 0.63
0.38 0.87 0.69
0.39 0.87 0.70
0.41 0.80 0.80
0.45 0.80 0.81
0.48 0.78 0.83
0.51 0.76 0.83
0.55 0.76 0.85
0.60 0.74 0.85
0.69 0.69 0.87
0.79 0.65 0.91
0.83 0.63 0.91
0.84 0.61 0.91
Inf 0.00 1.00

La courbe ROC peut également être présentée de même que l’aire sous la courbe (l’AUC) à l’aide de la fonction plot.roc() de la librairie pROC.

plot.roc(roc_data, 
         print.auc = TRUE, 
         grid = TRUE)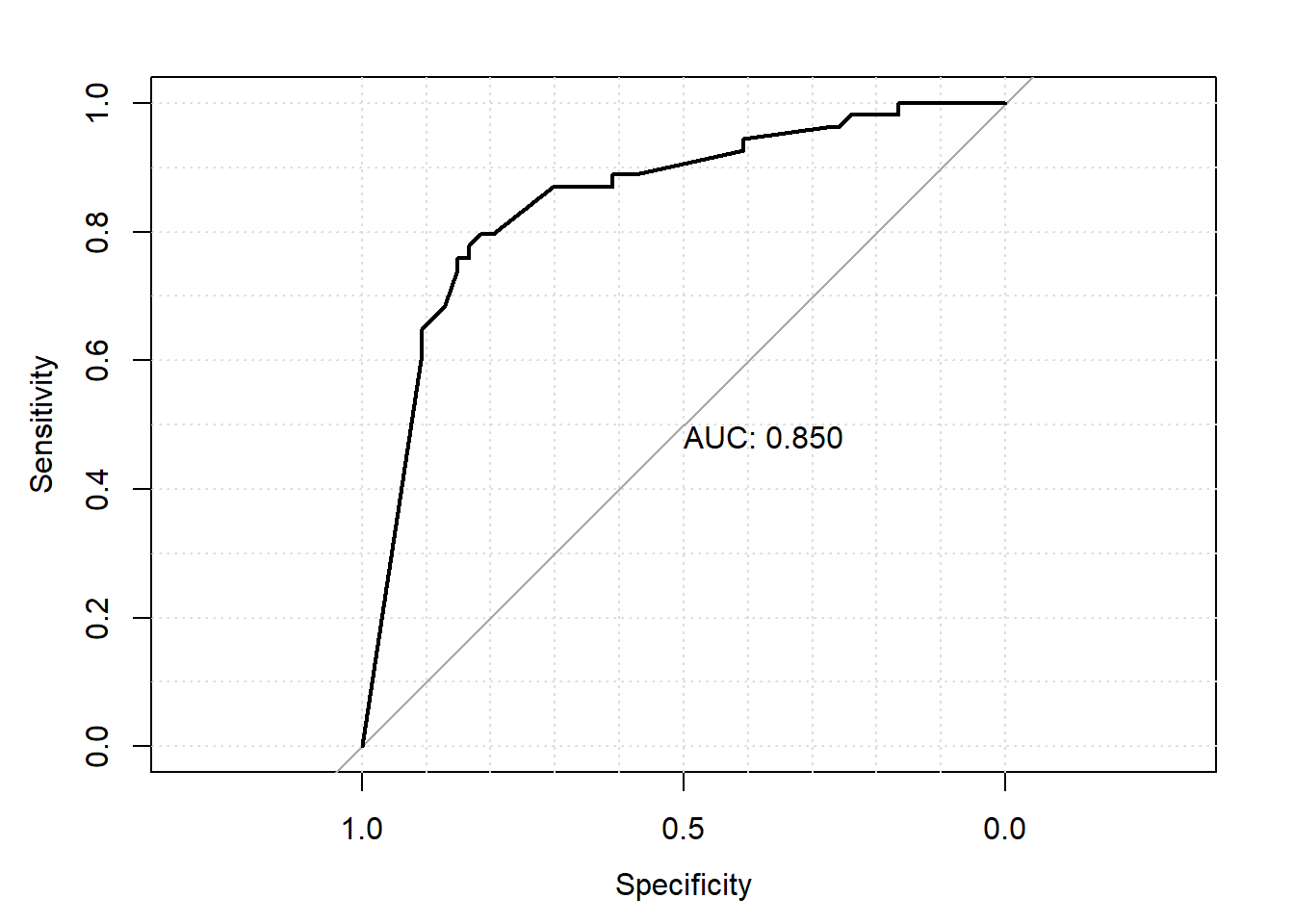
Courbe ROC.

Figure 7.5: Courbe ROC.

À l’aide de la table accu que vous avez produite précédemment à l’aide de l’objet ROC créé, vous pourrez produire différents graphiques par exemple des graphiques illustrant comment la sensibilité (et/ou la spécificité) varie en fonction du seuil choisi.

library(ggplot2)

#En premier lieu, nous pouvons demander une figure du seuil de probabilité (en x) par la sensibilité (en y)
ggplot(accu,
       aes(x=Seuil,
           y=Se)
       ) +
  geom_line() +
#Et nous pouvons ajouter une 2e ligne (pointillée dans ce cas), pour la spécificité
  geom_line(aes(y=Sp),
            linetype = "dashed") +
#Finalement, ajuster les éléments de format de la figure
  ylab("Précision diagnostique (Se ou Sp)") +
  xlab("Seuil de probabilité prédite par le modèle") +
  theme_bw()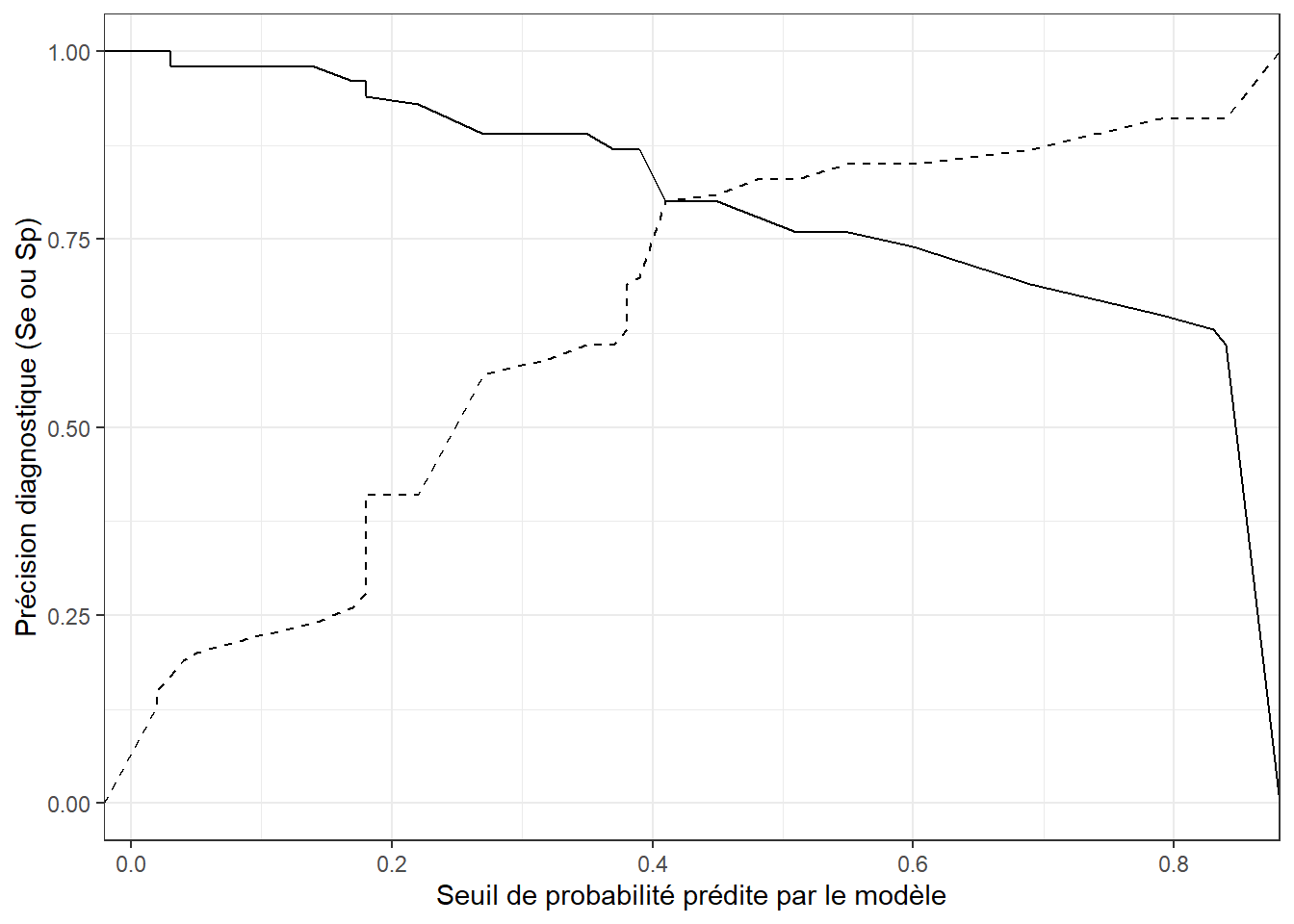
Sensibilité (ligne continue) et spécificité (ligne pointillée) du modèle en fonction du seuil de probabilité prédite.

Figure 7.6: Sensibilité (ligne continue) et spécificité (ligne pointillée) du modèle en fonction du seuil de probabilité prédite.

7.14 Travaux pratiques 4 - Régression logistique - Base

7.14.1 Exercices

Pour ce TP utilisez le fichier Nocardia (voir description VER p.823).

Dans cette étude nous sommes intéressés à décrire la probabilité d’être un cas par rapport à un contrôle selon la proportion de vaches taries ayant reçu un traitement antibiotique ou ayant reçu de la cloxacilline, néomycine etc.

  1. Avant de réaliser la régression logistique, on peut tout d’abord faire des tabulations croisées et calculer les rapports de cotes (RC) et tests de chi-carré pour comprendre les relations entre la variable dépendante et les prédicteurs catégoriques d’intérêt (dneo, dclox et dbarn). Après inspection de ces tables, quelles sont vos premières conclusions quant à la relation entre l’utilisation de cloxacilline et la probabilité de nocardiose, de même qu’entre l’utilisation de néomycine et Nocardia ?

  2. Vous pourriez aussi tenter de visualiser et/ou tester comment dcpct varie en fonction du statut nocardia. Que notez-vous?

  3. Vous êtes intéressé par le modèle de régression logistique suivant qui évalue l’effet d’utiliser neomycine et/ou cloxacilline sur la probabilité de Nocardia en gardant constant le type de stabulation et le % de vaches traitées (facteurs confondants).

\(logit(Pcasecont=1) = β_0 + β_1*dneo + β_2*dclox + β_3*dbarn + β_4*dcpct\)

3.1. Évaluez ce modèle à l’aide de la fonction glm(). Assurez-vous d’indiquer le niveau de référence 0 pour la neomycine et la cloxacilline et le niveau de référence 1 (i.e. stabulation libre) pour le type de stabulation. Quelle est la valeur de chi-carré, le nombre de degrés de liberté et la valeur de P du test de rapport de vraisemblance? Quelles sont vos conclusions? Quel était le test équivalent en régression linéaire?
3.2. Comparez le modèle complet vs. un modèle sans la variable dbarn. Vous obtiendrez une valeur de P de 0.06. Dans vos tables de résultats précédentes, des valeurs de P de 0.03 et 0.85 sont rapportées pour dbarn 2 et dbarn 3, respectivement. Qu’indiquent ces différentes valeurs de P et quels étaient les tests équivalents en régression linéaire?
3.3. Quels sont le coefficient et le rapport de cotes de dcpct? Comment les interprétez-vous?
3.4. Quel serait le RC (et IC 95%) d’une augmentation de 15% de dcpct sur les odds de maladie?
3.5. Quel est le RC de dneo ?
3.6. Calculez l’IC 95% pour dneo? Comment interprétez-vous cet IC 95% et la valeur de P rapportée pour le test de Wald?

  1. La présence d’un biais de confusion peut être vérifiée en ajoutant la variable de confusion potentielle au modèle et ensuite en décidant si le coefficient de la variable d’intérêt a changé de manière substantielle. En assumant le diagramme causal suivant :

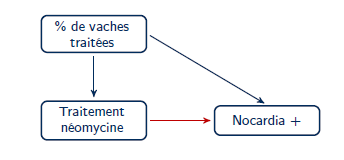
Figure 7.8. Diagramme causal de la relation entre utilisation de la néomycine et probabilité de mammite à Nocardia.

Évaluez le changement relatif de l’effet de dneo sur la probabilité de nocardiose lorsque le modèle est ajusté ou non pour dcpct. Jugez-vous que ce facteur confondant cause un biais important dans cette étude?

  1. Vous vous rappelez subitement que dans les modèles de régression, lorsque vous utilisez un prédicteur continu comme dcpct, celui-ci doit être linéairement associé avec votre variable dépendante (i.e. la relation est une droite).
    5.1. En régression logistique, c’est avec le RC ou le log odds que les variables sont linéairement associées?
    5.2. Vérifiez si la relation avec dcpct est linéaire. Quelles sont vos conclusions?

  2. Maintenant modélisez l’interaction entre neomycine et cloxacilline dans votre modèle avec dneo dclox dcpct et dbarn.
    6.1. Quelles seraient les odds de nocardiose (et IC 95%) dans les troupeaux où cloxacilline et néomycine sont utilisées vs. ceux où aucun de ces traitements n’est utilisé? Ces troupeaux sont-ils significativement différents?
    6.2. Quel serait les odds de nocardiose (et IC 95%) dans les troupeaux où cloxacilline et néomycine sont utilisés vs. ceux où seulement neomycine est utilisé? Ces troupeaux sont-ils significativement différents?

7.14.2 Code R et réponses

Pour ce TP utilisez le fichier Nocardia (voir description VER p.823).

#Nous importons ce jeu de données
nocardia <-read.csv(file="nocardia.csv", 
                    header=TRUE, 
                    sep=";")
head(nocardia)
##   id casecont numcow prod        bscc dbarn dout dcprep dcpct dneo dclox doth
## 1  1        0     16 20,1 446,2000122     2    1      4     0    0     0    1
## 2  2        0     16 22,3         214     2    1      3   100    1     0    1
## 3  3        0     18 24,9         260     2    1      3    25    0     0    1
## 4  4        0     18      184,1999969     1    1      3     1    0     0    1
## 5  5        0     20 34,5 61,40000153     2    1      3   100    0     1    0
## 6  6        0     21 22,7 80,19999695     1    1      3     0    0     0    0
#Nous indiquons les variables catégoriques dans le jeu de données
nocardia$dbarn <- factor(nocardia$dbarn) 
nocardia$dneo <- factor(nocardia$dneo) 
nocardia$dclox <- factor(nocardia$dclox) 
nocardia$casecont <- factor(nocardia$casecont)

Dans cette étude nous sommes intéressés à décrire la probabilité d’être un cas par rapport à un contrôle selon la proportion de vaches taries ayant reçu un traitement antibiotique ou ayant reçu de la cloxacilline, néomycine etc.

  1. Avant de réaliser la régression logistique, on peut tout d’abord faire des tabulations croisées et calculer les rapports de cotes (RC) et tests de chi-carré pour comprendre les relations entre la variable dépendante et les prédicteurs catégoriques d’intérêt (dneo, dclox et dbarn). Après inspection de ces tables, quelles sont vos premières conclusions quant à la relation entre l’utilisation de cloxacilline et la probabilité de nocardiose, de même qu’entre l’utilisation de néomycine et Nocardia ?
#Dans sjPlot la fonction tab_xtab est intéressante pour générer les table 2x2 et le test de chi-carré
library(sjPlot)
#Pour dneo
tab_xtab(var.row = nocardia$dneo, 
         var.col = nocardia$casecont, 
         title = "dneo*casecont")
dneo*casecont
dneo casecont Total
0 1
0 29 5 34
1 25 49 74
Total 54 54 108
χ2=22.707 · df=1 · φ=0.478 · p=0.000 
#Les valeurs dans cette table peuvent ensuite être utilisées dans epiR pour calculer les mesures d'association et les chi-carré
library(epiR)
## Warning: le package 'epiR' a été compilé avec la version R 4.2.2
dat <- matrix(c(49, 25, 5, 29), 
              nrow = 2, 
              byrow = TRUE)
rownames(dat) <- c("D+", "D-") 
colnames(dat) <- c("E+", "E-") 
epi.2by2(dat = as.table(dat), 
         method = "cross.sectional",
         conf.level = 0.95, 
         units = 100, 
         outcome = "as.columns")
##              Outcome +    Outcome -      Total               Prevalence *
## Exposed +           49           25         74     66.22 (54.28 to 76.81)
## Exposed -            5           29         34      14.71 (4.95 to 31.06)
## Total               54           54        108     50.00 (40.22 to 59.78)
## 
## Point estimates and 95% CIs:
## -------------------------------------------------------------------
## Prevalence ratio                               4.50 (1.97, 10.28)
## Odds ratio                                     11.37 (3.92, 32.95)
## Attrib prevalence in the exposed *             51.51 (35.45, 67.57)
## Attrib fraction in the exposed (%)            77.79 (49.29, 90.27)
## Attrib prevalence in the population *          35.29 (20.11, 50.48)
## Attrib fraction in the population (%)         70.59 (37.44, 86.17)
## -------------------------------------------------------------------
## Uncorrected chi2 test that OR = 1: chi2(1) = 24.725 Pr>chi2 = <0.001
## Fisher exact test that OR = 1: Pr>chi2 = <0.001
##  Wald confidence limits
##  CI: confidence interval
##  * Outcomes per 100 population units

Réponse: RC (IC 95%) neomycine: 11.4 (3.9, 33.0)
\(X^2\) : P < 0.001
Odds de Nocardia sont 11.4 fois plus élevé dans les troupeaux utilisants la néomycine.

#Pour dclox
tab_xtab(var.row = nocardia$dclox, 
         var.col = nocardia$casecont, 
         title = "dclox*casecont")
dclox*casecont
dclox casecont Total
0 1
0 35 46 81
1 19 8 27
Total 54 54 108
χ2=4.938 · df=1 · φ=0.235 · p=0.026 
library(epiR)
dat <- matrix(c(8, 19, 46, 35), 
              nrow = 2, 
              byrow = TRUE)
rownames(dat) <- c("D+", "D-") 
colnames(dat) <- c("E+", "E-") 
epi.2by2(dat = as.table(dat), 
         method = "cross.sectional",
         conf.level = 0.95, 
         units = 100, 
         outcome = "as.columns")
##              Outcome +    Outcome -      Total               Prevalence *
## Exposed +            8           19         27     29.63 (13.75 to 50.18)
## Exposed -           46           35         81     56.79 (45.31 to 67.76)
## Total               54           54        108     50.00 (40.22 to 59.78)
## 
## Point estimates and 95% CIs:
## -------------------------------------------------------------------
## Prevalence ratio                               0.52 (0.28, 0.96)
## Odds ratio                                     0.32 (0.13, 0.82)
## Attrib prevalence in the exposed *             -27.16 (-47.48, -6.84)
## Attrib fraction in the exposed (%)            -91.67 (-253.30, -3.98)
## Attrib prevalence in the population *          -6.79 (-21.12, 7.54)
## Attrib fraction in the population (%)         -13.58 (-25.64, -2.68)
## -------------------------------------------------------------------
## Uncorrected chi2 test that OR = 1: chi2(1) = 5.975 Pr>chi2 = 0.015
## Fisher exact test that OR = 1: Pr>chi2 = 0.025
##  Wald confidence limits
##  CI: confidence interval
##  * Outcomes per 100 population units

Réponse: RC (IC 95%) cloxacilline: 0.32 (0.13, 0.82)
\(X^2\) : P = 0.01
Odds de Nocardia dans les troupeaux utilisants la cloxacilline sont multipliés par un facteur de 0.32 (i.e. odds sont plus faibles).

#Pour dbarn
tab_xtab(var.row = nocardia$dbarn, 
         var.col = nocardia$casecont, 
         title = "dbarn*casecont")
dbarn*casecont
dbarn casecont Total
0 1
1 13 22 35
2 38 29 67
3 3 3 6
Total 54 54 108
χ2=3.523 · df=2 · Cramer’s V=0.181 · Fisher’s p=0.140

Réponse: Pour dbarn on remarque 22 cas/35, 29 cas/67 et 3 cas/6 dans les troupeaux en stabulation entravée, libre, et autre, respectivement. Pas d’association significative (\(X^2\) : P = 0.181).

  1. Vous pourriez aussi tenter de visualiser et/ou tester comment dcpct varie en fonction du statut nocardia. Que notez-vous?

Réponse: Ici nous pourrions simplement faire un box-plot de dcpct par casecont.

ggplot(data=nocardia, 
       aes(x=dcpct, 
           y=casecont)
       ) +
  geom_boxplot() +
  theme_classic() +
  coord_flip() #Par défaut R produit des box-plot horizontaux, coord_flip() permet de les mettre verticaux.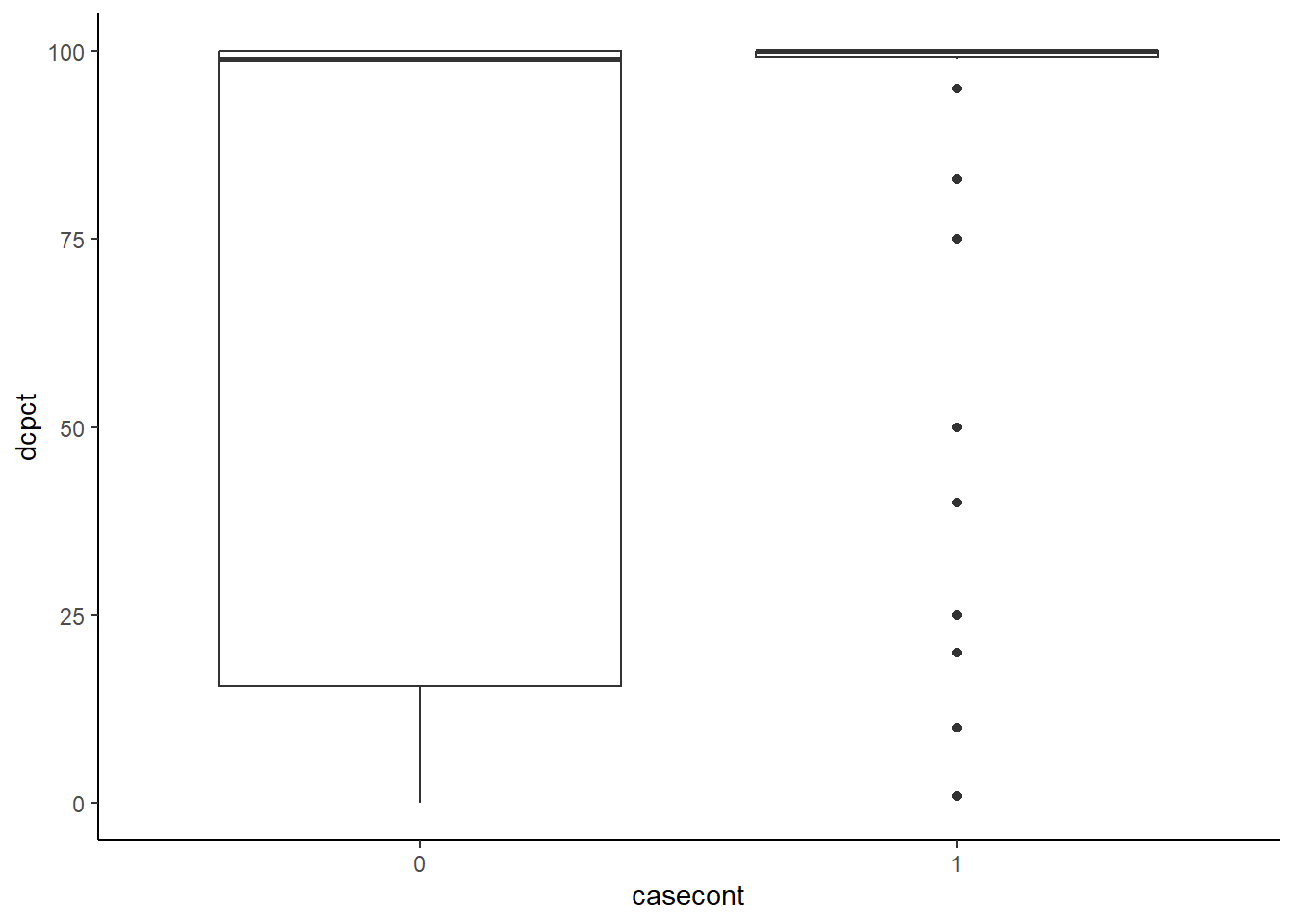
% de vaches traitées au tarissement dans un troupeau en fonction de son statut (cas vs témoin)

Figure 7.7: % de vaches traitées au tarissement dans un troupeau en fonction de son statut (cas vs témoin)

Nous pourrions aussi calculer la moyenne dans chacun des groupes (cas vs. témoin) et vérifier si cette moyenne varie en fonction du groupe. Dans le code plus bas le signe %>% indique à R une séquence d’actions à faire (aussi appellé un “pipeline”). Dans ce cas nous demandons de: 1) prendre l’objet nocardia (un jeu de données); 2) grouper les observations par niveau de la variable casecont (group_by); 3) dans ces groupes, calculer la moyenne et la médiane de la variable dcpct et appeller ces valeurs “Moyenne” et “Médiane”.

#Calculer la moyenne par groupe:
library(dplyr)
nocardia %>%
  group_by(casecont) %>%
  summarize(Moyenne=mean(dcpct), 
            Médiane=median(dcpct))
## # A tibble: 2 × 3
##   casecont Moyenne Médiane
##   <fct>      <dbl>   <dbl>
## 1 0           63.7      99
## 2 1           87.5     100

Réponse: On voit dans les figures que la majorité des troupeaux “cas” traitaient 100% des vaches alors que, pour les troupeaux “témoins”, il y avait un peu plus de troupeaux avec moins de 100% de vaches traitées. Les moyennes et médianes sont respectivement 88% et 100% pour les troupeaux cas et 64% et 99% pour les troupeaux témoins.

  1. Vous êtes intéressé par le modèle de régression logistique suivant qui évalue l’effet d’utiliser neomycine et/ou cloxacilline sur la probabilité de Nocardia en gardant constant le type de stabulation et le % de vaches traitées (facteurs confondants).

\(logit(P de casecont=1) = β_0 + β_1*dneo + β_2*dclox + β_3*dbarn + β_4*dcpct\)

3.1. Évaluez ce modèle à l’aide de la fonction glm(). Assurez-vous d’indiquer le niveau de référence 0 pour la neomycine et la cloxacilline et le niveau de référence 1 (i.e. stabulation libre) pour le type de stabulation. Quelle est la valeur de chi-carré, le nombre de degrés de liberté et la valeur de P du test de rapport de vraisemblance? Quelles sont vos conclusions? Quel était le test équivalent en régression linéaire?

#Placons d'abord les niveaux de référence
nocardia$dneo <- nocardia$dneo<-relevel(nocardia$dneo, ref="0")
nocardia$dclox <- nocardia$dclox<-relevel(nocardia$dclox, ref="0")
nocardia$dbarn <- nocardia$dbarn<-relevel(nocardia$dbarn, ref="1")

#Le modèle:
modele_1 <- glm(data=nocardia, 
                casecont ~ dneo + dclox + dbarn + dcpct, 
                family="binomial"
                )
library(lmtest)
lrtest(modele_1)
## Likelihood ratio test
## 
## Model 1: casecont ~ dneo + dclox + dbarn + dcpct
## Model 2: casecont ~ 1
##   #Df  LogLik Df  Chisq Pr(>Chisq)    
## 1   6 -51.158                         
## 2   1 -74.860 -5 47.403  4.702e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Réponse: La valeur de chi-carré est 47.4 avec 5 degrés de liberté. La valeur de P est < 0.001. Au moins un des coefficients est différent de zéro. Le test équivalent en régression linéaire est le test de F.

3.2. Comparez le modèle complet vs. un modèle sans la variable dbarn. Vous obtiendrez une valeur de P de 0.06. Dans vos tables de résultats précédentes, des valeurs de P de 0.03 et 0.85 sont rapportées pour dbarn 2 et dbarn 3, respectivement. Qu’indiquent ces différentes valeurs de P et quels étaient les tests équivalents en régression linéaire?

modele_red <- glm(data=nocardia, 
                  casecont ~ dneo + dclox + dcpct, 
                  family="binomial"
                  )
lrtest(modele_1, 
       modele_red)
## Likelihood ratio test
## 
## Model 1: casecont ~ dneo + dclox + dbarn + dcpct
## Model 2: casecont ~ dneo + dclox + dcpct
##   #Df  LogLik Df  Chisq Pr(>Chisq)  
## 1   6 -51.158                       
## 2   4 -53.994 -2 5.6707     0.0587 .
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(modele_1)
## 
## Call:
## glm(formula = casecont ~ dneo + dclox + dbarn + dcpct, family = "binomial", 
##     data = nocardia)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.6949  -0.7853   0.1021   0.7692   2.6801  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -2.445696   0.854328  -2.863  0.00420 ** 
## dneo1        2.685280   0.677273   3.965 7.34e-05 ***
## dclox1      -1.235266   0.580976  -2.126  0.03349 *  
## dbarn2      -1.333732   0.631925  -2.111  0.03481 *  
## dbarn3      -0.218350   1.154293  -0.189  0.84996    
## dcpct        0.021604   0.007657   2.821  0.00478 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 149.72  on 107  degrees of freedom
## Residual deviance: 102.32  on 102  degrees of freedom
## AIC: 114.32
## 
## Number of Fisher Scoring iterations: 5

Réponse: Le P de 0.06 indique que les coefficients des variables indicatrices utilisées pour modéliser la variable catégorique dbarn ne sont pas différent de zéro (i.e. globalement, dbarn n’est pas associé à la probabilité de nocardiose). Il s’agit d’un test de rapport de vraisemblance comparant modèles complet et réduit et ce test est équivalent au test de F comparant modèles complet et réduit en régression linéaire.
La valeur de P de 0.03 indique que le coefficient de dbarn2 (comparant cette catégorie à dbarn1) est différent de zéro. La valeur de P de 0.85 indique que le coefficient de dbarn3 (comparant cette catégorie à dbarn1) n’est pas différent de zéro. Il s’agit de tests de \(X^2\) de Wald et ils sont équivalents au test de T en régression linéaire. Normalement, on évaluerait d’abord le test global (rapport de vraissemblance) et, dans ce cas, on ne regarderait pas alors les valeurs individuelles puisque ce premier test n’est pas significatif.

3.3. Quels sont le coefficient et le rapport de cotes de dcpct? Comment les interprétez-vous?

library(jtools)
j <- summ(modele_1, 
          confint = TRUE)
#Les coefficients:
round(j$coeftable, 
      digits=3)
##               Est.   2.5%  97.5% z val.     p
## (Intercept) -2.446 -4.120 -0.771 -2.863 0.004
## dneo1        2.685  1.358  4.013  3.965 0.000
## dclox1      -1.235 -2.374 -0.097 -2.126 0.033
## dbarn2      -1.334 -2.572 -0.095 -2.111 0.035
## dbarn3      -0.218 -2.481  2.044 -0.189 0.850
## dcpct        0.022  0.007  0.037  2.821 0.005
#Les rapports de cotes:
round(exp(j$coeftable),
      digits=2)
##              Est. 2.5% 97.5% z val.    p
## (Intercept)  0.09 0.02  0.46   0.06 1.00
## dneo1       14.66 3.89 55.30  52.71 1.00
## dclox1       0.29 0.09  0.91   0.12 1.03
## dbarn2       0.26 0.08  0.91   0.12 1.04
## dbarn3       0.80 0.08  7.72   0.83 2.34
## dcpct        1.02 1.01  1.04  16.80 1.00

Réponse: Coefficient=0.022; le log odds d’être malade augmente de 0.022 unité par augmentation d’une unité (i.e. de 1%) du nombre de vaches traitées.
RC=1.02; les odds de nocardia sont multipliées par 1.02 (l’exposant de 0.022) par augmentation d’une unité (i.e. de 1%) du nombre de vaches traitées.

3.4. Quel serait le RC (et IC 95%) d’une augmentation de 15% de dcpct sur les odds de maladie?

nocardia$dcpct15 <- nocardia$dcpct/15
modele15 <- glm(data=nocardia, 
                casecont ~ dneo + dclox + dbarn + dcpct15, 
                family="binomial")

library(jtools)
j <- summ(modele15, 
          confint = TRUE)
#Les rapports de cotes:
round(exp(j$coeftable), 
      digits=2)
##              Est. 2.5% 97.5% z val.    p
## (Intercept)  0.09 0.02  0.46   0.06 1.00
## dneo1       14.66 3.89 55.30  52.71 1.00
## dclox1       0.29 0.09  0.91   0.12 1.03
## dbarn2       0.26 0.08  0.91   0.12 1.04
## dbarn3       0.80 0.08  7.72   0.83 2.34
## dcpct15      1.38 1.10  1.73  16.80 1.00

Réponse: RC (IC95): 1.38 (1.10, 1.73)

3.5. Quel est le RC de dneo ?
Réponse: RC: 14.66

3.6. Calculez l’IC 95% pour dneo? Comment interprétez-vous cet IC 95% et la valeur de P rapportée pour le test de Wald?
Réponse: IC95: (3.89, 55.30). L’IC 95% indique que le RC de dneo est différent de 1 (i.e. l’utilisation de néomycine est associée statistiquement à la probabilité de nocardiose). Le test de \(X^2\) de Wald indique que le coefficient de régression de dneo est différent de zéro (i.e. l’utilisation de néomycine est associée statistiquement à la probabilité de nocardiose).

  1. La présence d’un biais de confusion peut être vérifiée en ajoutant la variable de confusion potentielle au modèle et ensuite en décidant si le coefficient de la variable d’intérêt a changé de manière substantielle. En assumant le diagramme causal suivant :

Figure 7.6. Diagramme causal de la relation entre utilisation de la néomycine et probabilité de mammite à Nocardia.

Évaluez le changement relatif de l’effet de dneo sur la probabilité de nocardiose lorsque le modèle est ajusté ou non pour dcpct. Jugez-vous que ce facteur confondant cause un biais important dans cette étude?

Sur l’échelle log odds:

modele_incond <- glm(data=nocardia, 
                     casecont ~ dneo, 
                     family="binomial"
                     )
modele_cond_dcpct <- glm(data=nocardia, 
                         casecont ~ dneo + dcpct, 
                         family="binomial"
                         )

#Calculer différence relative sur l'échelle log odd
diff <- round(100*(modele_incond$coefficients[2]-modele_cond_dcpct$coefficients[2])/modele_incond$coefficients[2],
              digits=1)
#Créer une table avec log odds inconditionnelle, conditionnelle et diff relative 
cbind(inconditionnelle=modele_incond$coefficients[2], 
      conditionnelle=modele_cond_dcpct$coefficients[2], 
      Difference_relative=diff)
##       inconditionnelle conditionnelle Difference_relative
## dneo1         2.430802       2.400661                 1.2

Sur l’échelle RC:

#Calculer différence relative sur l'échelle RC
diff <- round(100*((exp(modele_incond$coefficients[2])-exp(modele_cond_dcpct$coefficients[2]))/exp(modele_incond$coefficients[2])), 
              digits=2)
#Créer une table avec log odds de l'analyse inconditionnelle, conditionnelle et la diff relative 
cbind(inconditionnelle=exp(modele_incond$coefficients[2]), 
      conditionnelle=exp(modele_cond_dcpct$coefficients[2]), 
      Difference_relative=diff)
##       inconditionnelle conditionnelle Difference_relative
## dneo1           11.368       11.03047                2.97

Réponse: D’une manière ou d’une autre, le biais semble minime (i.e. < 3% de différence dans nos estimés).

  1. Vous vous rappelez subitement que dans les modèles de régression, lorsque vous utilisez un prédicteur continu comme dcpct, celui-ci doit être linéairement associé avec votre variable dépendante (i.e. la relation est une droite).
    5.1. En régression logistique, c’est avec le RC ou le log odds que les variables sont linéairement associées?
    Réponse:: Avec le log odds (i.e. \(log(P/(1-P))\)
    5.2. Vérifiez si la relation avec dcpct est linéaire. Quelles sont vos conclusions?
#Nous pourrions créer des variables au carré et au cube de dcpct après l'avoir centré sur valeur moyenne (75%)
nocardia$dcpct_ct <- nocardia$dcpct-75
nocardia$dcpct_ct_sq <- nocardia$dcpct_ct*nocardia$dcpct_ct
nocardia$dcpct_ct_cu <- nocardia$dcpct_ct*nocardia$dcpct_ct*nocardia$dcpct_ct

#Vérifions le modèle avec terme au carré (pour voir s'il y a une courbe)
modele_carre <- glm(data=nocardia, 
                    casecont ~ dcpct_ct + dcpct_ct_sq, 
                    family="binomial"
                    )
summary(modele_carre)
## 
## Call:
## glm(formula = casecont ~ dcpct_ct + dcpct_ct_sq, family = "binomial", 
##     data = nocardia)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.3821  -1.3332   0.2478   1.0292   2.0633  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)
## (Intercept)  0.4503912  0.4348605   1.036    0.300
## dcpct_ct     0.0056391  0.0119672   0.471    0.637
## dcpct_ct_sq -0.0003716  0.0002956  -1.257    0.209
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 149.72  on 107  degrees of freedom
## Residual deviance: 136.50  on 105  degrees of freedom
## AIC: 142.5
## 
## Number of Fisher Scoring iterations: 4

Réponse: On peut vérifier si la relation est linéaire en ajoutant \(dcpct^2\), puis, si nécessaire, \(dcpct^2\) et \(dcpct^3\) au modèle. Bien sûr, ce n’est pas une mauvaise idée de centrer dcpct (sur sa moyenne par exemple) avant de faire ces transformations afin d’éviter toute colinéarité. Dans ce cas, le coefficient pour \(dcpct^2\) n’est pas significatif (P = 0.21). Une courbe ne semble donc pas être nécessaire. C’est donc probablement inutile d’aller vérifier si de multiples points d’inflexions (i.e. \(dcpct^3\)) sont nécessaires. Si vous l’avez tout de même fait, vous aurez noté des valeurs de P de 0.68 et de 0.40 pour les termes au carré et au cube, respectivement. Donc la relation entre dcpct et le log odds de nocardiose semble être linéaire et pourra être modélisée sans l’ajout de termes polynomiaux.

  1. Maintenant modélisez l’interaction entre neomycine et cloxacilline dans votre modèle avec dneo dclox dcpct et dbarn.
modele_inter <- glm(data=nocardia, 
                    casecont ~ dneo*dclox + dbarn + dcpct, 
                    family="binomial"
                    )

6.1. Quelles seraient les odds de nocardiose (et IC 95%) dans les troupeaux où cloxacilline et néomycine sont utilisées vs. ceux où aucun de ces traitements ne sont utilisés? Ces troupeaux sont-ils significativement différents?

library(emmeans)
contrast <- emmeans(modele_inter, 
                    c("dneo", 
                      "dclox")
                    ) 
confint(pairs(contrast, 
              type="response")
        ) 
##  contrast                    odds.ratio      SE  df asymp.LCL asymp.UCL
##  dneo0 dclox0 / dneo1 dclox0     0.0215  0.0206 Inf   0.00182     0.254
##  dneo0 dclox0 / dneo0 dclox1     0.4266  0.4635 Inf   0.02617     6.954
##  dneo0 dclox0 / dneo1 dclox1     0.1573  0.1695 Inf   0.00988     2.504
##  dneo1 dclox0 / dneo0 dclox1    19.8672 16.5247 Inf   2.34494   168.323
##  dneo1 dclox0 / dneo1 dclox1     7.3257  5.0901 Inf   1.22922    43.659
##  dneo0 dclox1 / dneo1 dclox1     0.3687  0.3452 Inf   0.03329     4.084
## 
## Results are averaged over the levels of: dbarn 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 4 estimates 
## Intervals are back-transformed from the log odds ratio scale

Réponse: Ce serait la 3ième ligne de la table précédente. Donc RC (IC95): 0.16 (0.01, 2.5). Comme la valeur nulle (1.0) est incluse dans l’IC95, il n’y a pas de différence significative dans les odds de nocardia entre ces deux types de troupeau.

6.2. Quel serait les odds de nocardiose (et IC 95%) dans les troupeaux où cloxacilline et néomycine sont utilisés vs. ceux où seulement neomycine est utilisé? Ces troupeaux sont-ils significativement différents?
Réponse: Ce serait la 5ième ligne de la table précédente. Donc RC (IC95): 7.3 (1.2, 43.7). Comme la valeur nulle (1.0) n’est pas incluse dans l’IC95, il y a une différence significative dans les odds de nocardia entre ces deux types de troupeau.

7.15 Travaux pratiques 5 - Régression logistique - Évaluation du modèle

7.15.1 Exercices

Pour ce TP utilisez le fichier Nocardia (voir description VER p.823).

Utilisez le modèle suivant: \(logit(Pcasecont=1) = β_0 + β_1*dneo + β_2*dclox + β_3*dneo*dclox + β_4*dcpct\)

  1. Lorsqu’une interaction est présente, il devient difficile de présenter clairement vos résultats. À l’aide de la fonction pairs() du package emmeans vous seriez cependant capable de créer une table comme proposée dans Knol et VanderWeele (2012) 5. Une autre manière consisterait à présenter l’effet de vos prédicteurs graphiquement sur une échelle de probabilité. Présentez ce graphique. Quel groupe de troupeaux se démarque particulièrement des autres en terme de probabilité de nocardiose?

  1. Évaluez l’adéquation du modèle. Quels sont les résultats et votre interprétation du test de Hosmer-Lemeshow?

  2. La valeur prédictive d’un modèle peut également être évaluée à l’aide d’une courbe ROC. Représenter graphiquement la courbe ROC. Quelle est l’aire sous la courbe pour votre modèle ? Quelles seraient la sensibilité et la spécificité de votre modèle si on fixe un seuil de 50% (i.e. si modèle prédit probabilité de nocardiose > 50% alors on diagnostique le troupeau comme nocardia positif)?

  3. Quel est le profil d’observation avec le résiduel de Pearson le plus élevé? Combien y-a-t-il d’observations dans ce profil?

  4. Quel profil d’observation avait le plus d’influence sur le coefficient de régression de dcpct? Pourquoi à votre opinion?

7.15.2 Code R et réponses

Pour ce TP utilisez le fichier Nocardia (voir description VER p.823).

#Nous importons ce jeu de données
nocardia <-read.csv(file="nocardia.csv", 
                    header=TRUE, 
                    sep=";"
                    )
head(nocardia)
##   id casecont numcow prod        bscc dbarn dout dcprep dcpct dneo dclox doth
## 1  1        0     16 20,1 446,2000122     2    1      4     0    0     0    1
## 2  2        0     16 22,3         214     2    1      3   100    1     0    1
## 3  3        0     18 24,9         260     2    1      3    25    0     0    1
## 4  4        0     18      184,1999969     1    1      3     1    0     0    1
## 5  5        0     20 34,5 61,40000153     2    1      3   100    0     1    0
## 6  6        0     21 22,7 80,19999695     1    1      3     0    0     0    0
#Nous indiquons les variables catégoriques dans le jeu de données
nocardia$dbarn <- factor(nocardia$dbarn) 
nocardia$dneo <- factor(nocardia$dneo) 
nocardia$dclox <- factor(nocardia$dclox) 
nocardia$casecont <- factor(nocardia$casecont)

Utilisez le modèle suivant: \(logit(Pcasecont=1) = β_0 + β_1*dneo + β_2*dclox + β_3*dneo*dclox + β_4*dcpct\)

modele <- glm(data = nocardia, 
              casecont ~ dneo*dclox + dcpct, 
              family = binomial
              )
  1. Lorsqu’une interaction est présente, il devient difficile de présenter clairement vos résultats. À l’aide de la fonction pairs() du package emmeans vous seriez cependant capable de créer une table comme proposée dans Knol et VanderWeele (2012). Une autre manière consisterait à présenter l’effet de vos prédicteurs graphiquement sur une échelle de probabilité. Présentez ce graphique. Quel groupe de troupeaux se démarque particulièrement des autres en terme de probabilité de nocardiose?
library(sjPlot)
plot_model(modele, 
           type="eff", 
           terms=c("dcpct", 
                   "dneo", 
                   "dclox")
           )
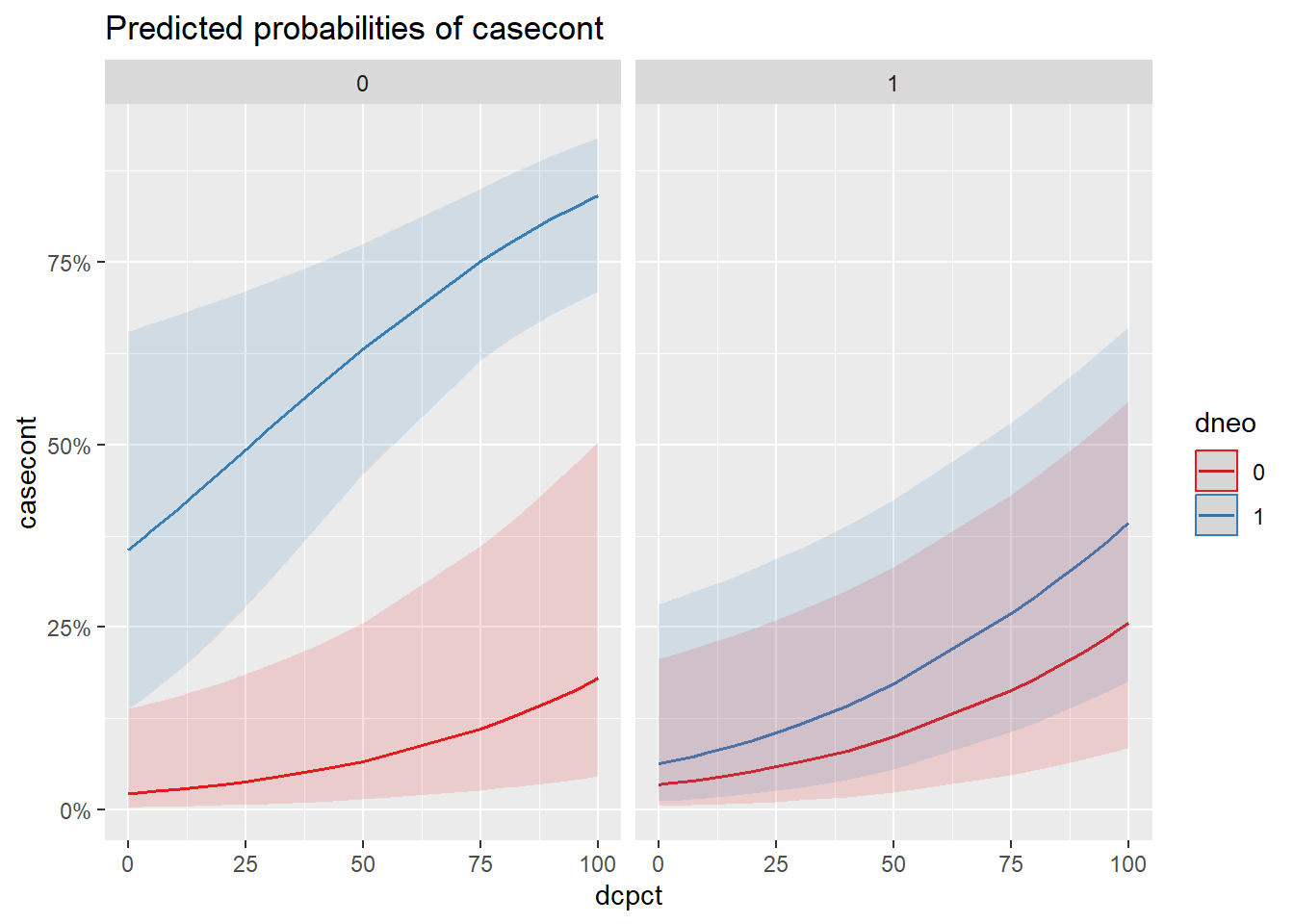
Effet sur la probabilité de nocardia de l'utilisation de la neomycine et du % de vache traitées au tarissement par niveau d'utilisation de la cloxacilline.

Figure 7.8: Effet sur la probabilité de nocardia de l’utilisation de la neomycine et du % de vache traitées au tarissement par niveau d’utilisation de la cloxacilline.

Réponse: Les troupeaux utilisant seulement la néomycine (sans cloxacilline) semblent avoir une probabilité beaucoup plus élevée de nocardiose.

  1. Évaluez l’adéquation du modèle. Quels sont les résultats et votre interprétation du test de Hosmer-Lemeshow?

Réponse:

library(ResourceSelection)
hoslem.test(modele$y, 
            fitted(modele), 
            g=8
            )
## 
##  Hosmer and Lemeshow goodness of fit (GOF) test
## 
## data:  modele$y, fitted(modele)
## X-squared = 1.4887, df = 6, p-value = 0.9602

Interprétation: Le modèle est adéquat (P=0.96).

  1. La valeur prédictive d’un modèle peut également être évaluée à l’aide d’une courbe ROC. Représenter graphiquement la courbe ROC. Quelle est l’aire sous la courbe pour votre modèle ? Quelles seraient la sensibilité et la spécificité de votre modèle si on fixe un seuil de 50% (i.e. si modèle prédit probabilité de nocardiose > 50% alors on diagnostique le troupeau comme nocardia positif)?
library(broom)
diag <- augment(modele) #Nous venons de créer une nouvelle table dans laquelle les résiduels, distance de cook, etc se trouvent maintenant

#Nous ajoutons les valeurs prédites de l'objet modele
diag$pred_prob <- modele$fitted.values

#Nous génèrons l'objet ROC.
library(pROC)
roc_data <- roc(data=diag, 
                response="casecont", 
                predictor="pred_prob"
                )

#Puis la courbe ROC
plot.roc(roc_data, 
         print.auc = TRUE, 
         grid = TRUE)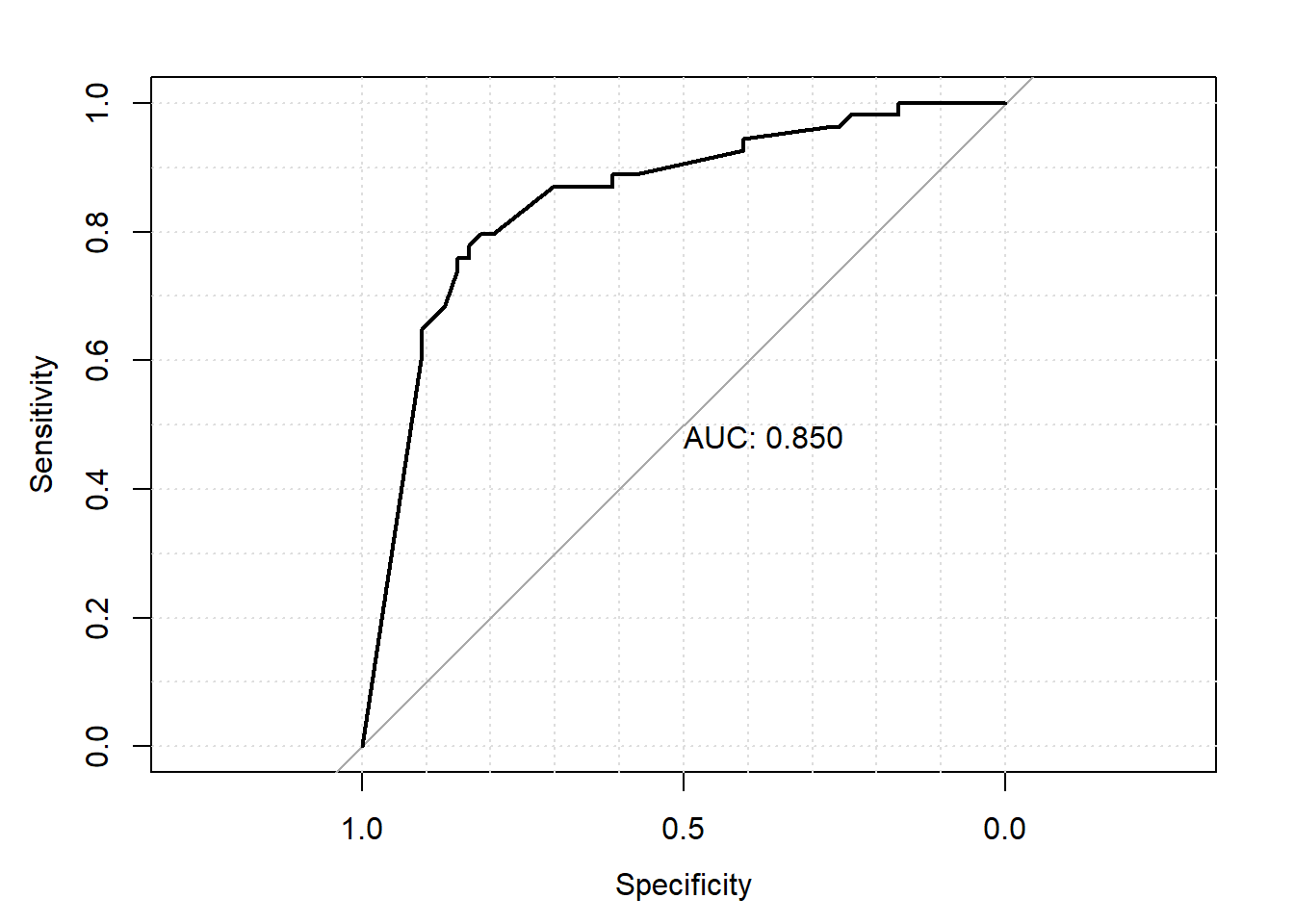
Courbe ROC.

Figure 7.9: Courbe ROC.

Réponse: L’aire sous la courbe est 0.850. Avec une table, ce sera facile de trouver les Se et Sp pour différents seuils.

#Présenter les sensibilités et spécificités des différents seuils dans une même table.
accu <- as.data.frame(round(cbind(Seuil=roc_data$thresholds, 
                    Se=roc_data$sensitivities, 
                    Sp=roc_data$specificities), 
              digits=2))

#Voir la table
library(knitr)
library(kableExtra)
kable(accu,  
      caption="Sensibilité et spécificité du modèle pour différents seuils de probabilité prédite.")%>%
  kable_styling()
Table 7.4: Sensibilité et spécificité du modèle pour différents seuils de probabilité prédite.
Seuil Se Sp
-Inf 1.00 0.00
0.02 1.00 0.13
0.02 1.00 0.15
0.03 1.00 0.17
0.03 0.98 0.17
0.04 0.98 0.19
0.05 0.98 0.20
0.09 0.98 0.22
0.14 0.98 0.24
0.17 0.96 0.26
0.18 0.96 0.28
0.18 0.94 0.41
0.22 0.93 0.41
0.27 0.89 0.57
0.32 0.89 0.59
0.35 0.89 0.61
0.37 0.87 0.61
0.38 0.87 0.63
0.38 0.87 0.69
0.39 0.87 0.70
0.41 0.80 0.80
0.45 0.80 0.81
0.48 0.78 0.83
0.51 0.76 0.83
0.55 0.76 0.85
0.60 0.74 0.85
0.69 0.69 0.87
0.79 0.65 0.91
0.83 0.63 0.91
0.84 0.61 0.91
Inf 0.00 1.00

Réponse: On note des Se et Sp de 0.76 et 0.83, respectivement lorsqu’on fixe le seuil de probabilité à >0.50 (en fait 0.51 et plus).

  1. Quel est le profil d’observations avec le résiduel de Pearson le plus élevé? Combien y-a-t-il d’observations dans ce profil?
#Nous pourrions maintenant ordonner cette table pour voir les 10 observations avec les résiduels les plus larges
diag_maxres <- diag[order(-diag$.resid),]
head(diag_maxres, 10)
## # A tibble: 10 × 11
##    casecont dneo  dclox dcpct .fitted .resid .std.resid   .hat .sigma .cooksd
##    <fct>    <fct> <fct> <int>   <dbl>  <dbl>      <dbl>  <dbl>  <dbl>   <dbl>
##  1 1        0     0        10  -3.55    2.68       2.71 0.0243  0.971  0.178 
##  2 1        1     1        50  -1.57    1.87       1.93 0.0592  0.989  0.0641
##  3 1        0     0       100  -1.52    1.85       1.94 0.0901  0.988  0.0990
##  4 1        0     1        83  -1.45    1.82       1.89 0.0707  0.989  0.0700
##  5 1        0     1       100  -1.07    1.65       1.73 0.0847  0.992  0.0589
##  6 1        0     1       100  -1.07    1.65       1.73 0.0847  0.992  0.0589
##  7 1        1     0         1  -0.570   1.43       1.50 0.0893  0.996  0.0381
##  8 1        1     1       100  -0.437   1.37       1.42 0.0757  0.997  0.0275
##  9 1        1     1       100  -0.437   1.37       1.42 0.0757  0.997  0.0275
## 10 1        1     1       100  -0.437   1.37       1.42 0.0757  0.997  0.0275
## # … with 1 more variable: pred_prob <dbl>

Réponse: Le modèle prédit une probabilité de moins de 3% de nocardiose dans un troupeau qui n’utilise ni neomycine, ni cloxacilline et où 10% des vaches sont traitées au tarissement. Il y a une seule observation dans ce profil et il s’agit d’un troupeau positif à nocardia (d’où le résiduel très large).

  1. Quel profil d’observations avait le plus d’influence sur le coefficient de régression de dcpct? Pourquoi à votre opinion?
#Nous pourrions maintenant ordonner cette table pour voir les 10 observations avec les leviers les plus larges
diag_cook <- diag[order(-diag$.cooksd),]
head(diag_cook, 10)
## # A tibble: 10 × 11
##    casecont dneo  dclox dcpct .fitted .resid .std.resid   .hat .sigma .cooksd
##    <fct>    <fct> <fct> <int>   <dbl>  <dbl>      <dbl>  <dbl>  <dbl>   <dbl>
##  1 1        0     0        10  -3.55    2.68       2.71 0.0243  0.971  0.178 
##  2 1        0     0       100  -1.52    1.85       1.94 0.0901  0.988  0.0990
##  3 1        0     1        83  -1.45    1.82       1.89 0.0707  0.989  0.0700
##  4 1        1     1        50  -1.57    1.87       1.93 0.0592  0.989  0.0641
##  5 1        0     1       100  -1.07    1.65       1.73 0.0847  0.992  0.0589
##  6 1        0     1       100  -1.07    1.65       1.73 0.0847  0.992  0.0589
##  7 1        1     0         1  -0.570   1.43       1.50 0.0893  0.996  0.0381
##  8 1        1     1       100  -0.437   1.37       1.42 0.0757  0.997  0.0275
##  9 1        1     1       100  -0.437   1.37       1.42 0.0757  0.997  0.0275
## 10 1        1     1       100  -0.437   1.37       1.42 0.0757  0.997  0.0275
## # … with 1 more variable: pred_prob <dbl>

Réponse: C’est le même profil identifié à la question 5. En général, une augmentation de dcpct entraine une augmentation de la probabilité de nocardia, mais cette observation à un dcpct bas (10% ; le 15ième plus bas du jeu de donnée), mais le troupeau était tout de même un troupeau cas. Ce profil tire donc la droite de régression vers lui (et modifie donc le coefficient de régression).

  1. Recommendations for presenting analyses of effect modification and interaction. M. J. Knol and T. J. VanderWeele, Int J Epidemiol 2012 Vol. 41 Issue 2 Pages 514-20↩︎