Chapitre 8 Régression pour données de compte et d’incidence
Les régressions pour données de compte et d’incidence (e.g. Poisson, binomiale négative, zero-inflated Poisson (ZIP) et zero-inflated binomiale negative (ZINB)) peuvent être réalisées dans R avec différentes librairies et fonctions.
La figure suivante schématise les différentes méthodes qui pourront être utilisées.

Méthodes de régression pour données de compte et d’incidence.
Le jeu de données tb_real.csv sera utilisé pour cette section.
#Nous importons ce jeu de données
tb <-read.csv(file="tb_real.csv",
header=TRUE,
sep=";"
)
head(tb)## obs farm_id type sex age reactors par
## 1 1 4002 2 0 0 1 525
## 2 2 4002 2 0 1 2 3675
## 3 3 4002 2 0 2 5 5775
## 4 4 4002 2 1 1 3 2625
## 5 5 4002 2 1 2 1 525
## 6 6 4003 2 0 2 2 7824#Nous indiquons les variables catégoriques dans le jeu de données. Nous allons aussi ajouter des étiquettes pour faciliter l'interprétation plus tard.
tb$farm_id <- factor(tb$farm_id)
tb$type <- factor(tb$type,
levels=c(1,2,3,4),
labels=c("laitier",
"boucherie",
"cervidé",
"autre")
)
tb$sex <- factor(tb$sex,
levels=c(0,1),
labels=c("femelle",
"mâle")
)
tb$age <- factor(tb$age,
levels=c(0:2),
labels=c("0-12 mois",
"12-24 mois",
">24 mois")
)8.1 Régression de Poisson
La fonction glm() que vous avez déjà utilisée pour la régression logistique pourra effectuer la régression de Poisson lorsque la variable dépendante est simplement un compte d’événements, par exemple un nombre d’animaux positifs à un test de tuberculine dans un groupe d’animaux (i.e. la variable reactors dans le jeu de données tb_real.csv) et qu’il n’y a pas de dénominateur à prendre en considération (i.e., que le nombre d’animal-temps à risque ne varie pas par unité d’étude). Dans ce cas, on n’aura qu’à indiquer la famille (family="poisson"). Notez que la fonction glm() supposera automatiquement que la fonction de lien est le log et que la fonction de la variance est .
Par exemple, le modèle suivant permettrait d’effectuer une régression de Poisson avec les prédicteurs type, sex et age. D’abord en supposant que ce n’est pas nécessaire de prendre en compte un dénominateur (i.e. un nombre d’animal-temps à risque). Évidemment, cette supposition est incorrecte dans ce cas.
#En indiquant family="poisson", la fonction glm suppose une distribution de Poisson et un lien log
modele_incid <- glm( data=tb,
reactors ~ type + sex + age,
family="poisson")
summary(modele_incid)##
## Call:
## glm(formula = reactors ~ type + sex + age, family = "poisson",
## data = tb)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.2978 -1.4704 -0.4919 -0.1823 7.0686
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.4607 0.7333 -3.356 0.000792 ***
## typeboucherie -0.4311 0.2359 -1.828 0.067579 .
## typecervidé 0.3485 0.2237 1.558 0.119226
## typeautre -1.4651 0.6113 -2.397 0.016546 *
## sexmâle -1.2051 0.1850 -6.513 7.38e-11 ***
## age12-24 mois 3.0549 0.7219 4.232 2.32e-05 ***
## age>24 mois 3.8056 0.7121 5.344 9.10e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 664.82 on 133 degrees of freedom
## Residual deviance: 454.44 on 127 degrees of freedom
## AIC: 597.41
##
## Number of Fisher Scoring iterations: 6L’intercept et le coefficient de chacun des prédicteurs sont rapportés, de même que leur erreur-type, et la valeur de P correspondante.
8.1.1 Indiquer un “offset” (i.e., un dénominateur, par exemple un nombre d’animal-temps à risque)
Souvent, un dénominateur (e.g. un nombre d’animal-temps à risque par unité d’étude) doit être pris en compte pour les données d’incidence ou de compte. Par exemple, dans le jeu de données tb_real.csv, la variable par représente le nombre d’animal-jour à risque par groupe et l’on voit que celui-ci varie passablement (de 30 à 118 084 animal-jour à risque). Bien sûr, ce ne serait pas valide de donner le même poids à des groupes avec des dénominateurs passablement différents (e.g. 3 positifs/30 animal-jours à risque est très différent de 3 positifs/118 084 animal-jour à risque). Dans ce cas, on devra indiquer au modèle une variable offset (i.e. un terme qui ne sert qu’à calibrer le poids de chaque observation et pour lequel aucun coefficient de régression n’est calculé). L’option offset() permettra d’indiquer la variable qui servira d’offset. Notez que, puisque la transformation logarithmique est utilisée comme fonction de lien pour la régression de compte et d’incidence, vous devrez d’abord transformer de la même façon (i.e. faire le log naturel) de votre variable qui représentait le nombre d’animal-jour à risque. Cette nouvelle variable représentera le log du nombre d’animal-jour à risque.
Par exemple, le modèle suivant permettrait d’effectuer une régression de Poisson en prenant en compte le dénominateur (i.e. le nombre d’animal-temps à risque ; variable par dans ce cas) de chacun des troupeaux. Ce modèle serait, évidemment, plus approprié dans notre cas.
#En premier lieu créons une variable offset qui représentera le nombre d'animaux-jour à risque, mais sur une échelle logarithmique
tb$log_par<-log(tb$par)
#Nous devons indiquer cette variable directement dans le modèle avec + offset()
modele_incid <- glm(data=tb,
reactors ~ type + sex + age + offset(log_par),
family="poisson"
)
summary(modele_incid)##
## Call:
## glm(formula = reactors ~ type + sex + age + offset(log_par),
## family = "poisson", data = tb)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.5386 -0.8607 -0.3364 -0.0429 8.7903
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -11.6899 0.7398 -15.802 < 2e-16 ***
## typeboucherie 0.4422 0.2364 1.871 0.061410 .
## typecervidé 1.0662 0.2334 4.569 4.91e-06 ***
## typeautre 0.4384 0.6149 0.713 0.475898
## sexmâle -0.3619 0.1954 -1.852 0.064020 .
## age12-24 mois 2.6734 0.7217 3.704 0.000212 ***
## age>24 mois 2.6012 0.7136 3.645 0.000267 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 409.03 on 133 degrees of freedom
## Residual deviance: 348.35 on 127 degrees of freedom
## AIC: 491.32
##
## Number of Fisher Scoring iterations: 88.1.2 Test de rapport de vraisemblance
On pourra demander le test de rapport de vraisemblance comme vu en régression logistique.
library(lmtest)
lrtest(modele_incid) #test du rapport de vraisemblance du modèle## Likelihood ratio test
##
## Model 1: reactors ~ type + sex + age + offset(log_par)
## Model 2: reactors ~ 1
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 7 -238.66
## 2 1 -396.90 -6 316.47 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Dans ce cas, le modèle est significatif (P< 0.001).
8.1.3 Présenter les ratios d’incidence
En mettant à l’exposant les coefficients de régression, ils représenteront maintenant les ratios d’incidence (RI) lorsqu’un prédicteur continu augmente d’une unité ou pour un niveau d’un prédicteur catégorique comparativement au niveau de référence. Par exemple, on pourrait demander ces coefficients transformés et leur intervalle de confiance.
library(jtools)
#Nous utilisons la librairie jtools pour obtenir une table avec les coefficients et les IC95
j <- summ(modele_incid,
confint = TRUE
)
#Nous utilisons round() pour ajuster la précision des valeurs dans les tables
round(exp(j$coeftable),
digits=2
)## Est. 2.5% 97.5% z val. p
## (Intercept) 0.00 0.00 0.00 0.00 1.00
## typeboucherie 1.56 0.98 2.47 6.49 1.06
## typecervidé 2.90 1.84 4.59 96.42 1.00
## typeautre 1.55 0.46 5.17 2.04 1.61
## sexmâle 0.70 0.47 1.02 0.16 1.07
## age12-24 mois 14.49 3.52 59.62 40.61 1.00
## age>24 mois 13.48 3.33 54.59 38.28 1.00Par exemple, le RI de boucherie comparativement à la valeur de référence laitier est de 1.56 (IC95: 0.98, 2.47).
8.1.4 Calculer un compte prédit d’évènements
On pourra également demander le compte attendu d’évènements pour un individu avec un profil de prédicteurs donné. Il faudrait alors simplement additionner manuellement l’intercept, puis les niveaux des prédicteurs qui nous intéressent et, ensuite, mettre cette somme à l’exposant. Plus pratiquement, on pourra demander dans R une prédiction pour une combinaison donnée. Par exemple, dans le code qui suit nous génèrons un petit jeu de données qui contiendra les valeurs des prédicteurs pour lesquelles nous voudrons obtenir le compte prédit d’évènements. Par exemple, troupeau laitier (type=1), femelle (sex=0) et 0-12 mois d’âge (age=0). Nous avons aussi indiqué que la variable log_par (l’offset) prendrait la valeur log(100 000). On aura donc un compte d’évènements pour 100 000 animaux-jours à risque.
Puis, nous demandons simplement la prédiction à l’aide de la fonction predict(). Nous y indiquons l’objet modèle qui a préalablement été créé (modele_incid) et le petit jeu de données qui contient les valeurs que nous venons de créer (new.tb). Il ne reste qu’à mettre le tout à l’exposant avec la fonction exp().
#Nous générons le jeu de données avec les valeurs pour lesquelles nous voudrons obtenir le compte prédit d'évènements.
new.tb <- data.frame(type="laitier",
sex="femelle",
age="0-12 mois",
log_par=(log(100000)
)
)
#Nous générons la prédiction pour cette combinaison de prédicteurs.
exp(predict(modele_incid,
newdata=new.tb
)
)## 1
## 0.8378225Le modèle prédit donc 0.84 cas de TB par 100 000 animaux-jours à risque chez les troupeaux de femelles laitières de 0-12 mois.
8.1.5 Comparer les niveaux d’un prédicteur catégorique avec > 2 catégories
Comme pour la régression logistique, les fonctions emmeans() et pairs() du package emmeans vous permettent de comparer toutes les combinaisons possibles d’un ou plusieurs prédicteurs catégoriques et/ou quantitatifs.
Par exemple, le code suivant permet de comparer les catégories de la variable type entre elles. Notez qu’en indiquant type="response", les résultats seront présentés sous forme de ratio d’incidence (RI). Ils sont aussi déjà ajustés pour les comparaisons multiples avec l’ajustement de Tukey-Kramer.
library(emmeans)
contrast <- emmeans(modele_incid,
c("type")
)
confint(pairs(contrast,
type="response")
)## contrast ratio SE df asymp.LCL asymp.UCL
## laitier / boucherie 0.643 0.1519 Inf 0.350 1.180
## laitier / cervidé 0.344 0.0804 Inf 0.189 0.627
## laitier / autre 0.645 0.3967 Inf 0.133 3.131
## boucherie / cervidé 0.536 0.0888 Inf 0.350 0.820
## boucherie / autre 1.004 0.5958 Inf 0.219 4.612
## cervidé / autre 1.874 1.1002 Inf 0.414 8.469
##
## Results are averaged over the levels of: sex, age
## Confidence level used: 0.95
## Conf-level adjustment: tukey method for comparing a family of 4 estimates
## Intervals are back-transformed from the log scaleOn note, par exemple, que les laitiers ont une incidence 0.64 fois plus faible (IC95: 0.35, 1.18) que les boucheries. Si vous voulez voir les comparaisons dans l’autre sens (boucherie comparé à laitier, plutôt que laitier comparé à boucherie), vous pouvez ajouter l’option reverse=TRUE dans la fonction pairs().
library(emmeans)
contrast <- emmeans(modele_incid,
c("type")
)
confint(pairs(contrast,
reverse=TRUE,
type="response")
)## contrast ratio SE df asymp.LCL asymp.UCL
## boucherie / laitier 1.556 0.368 Inf 0.848 2.86
## cervidé / laitier 2.904 0.678 Inf 1.595 5.29
## cervidé / boucherie 1.866 0.309 Inf 1.219 2.86
## autre / laitier 1.550 0.953 Inf 0.319 7.52
## autre / boucherie 0.996 0.591 Inf 0.217 4.58
## autre / cervidé 0.534 0.313 Inf 0.118 2.41
##
## Results are averaged over the levels of: sex, age
## Confidence level used: 0.95
## Conf-level adjustment: tukey method for comparing a family of 4 estimates
## Intervals are back-transformed from the log scale8.1.6 Linéarité de la relation (pour prédicteur continu)
La linéarité de la relation est une supposition importante du modèle. Pour les prédicteurs continus, vous devrez toujours vérifier si cette supposition est bien respectée. Vous pouvez le faire simplement à l’aide du modèle polynomial, comme vu précédemment (en ajoutant le ou le et le dans votre modèle).
8.1.7 Test de chi-carré de Pearson
Nous pouvons calculer la somme des résiduels de de la façon suivante:
library(broom)
diag <- augment(modele_incid,
type.residuals = "pearson") #Nous venons de créer une nouvelle table avec les résiduels, etc.
#Nous calculons la somme de ces résiduels au carré. Dans ce cas: 1105.7
s <- sum(diag$.resid^2)
s## [1] 1105.703#Nous vérifions à quelle probabilité la valeur 1105.7 correspond dans une distribution de chi-carré avec les degrés de liberté (n - le nombre de coefficients-1).
P <- 1-pchisq(s,
df=(134-6-1)
)
P## [1] 0#Nous pouvons aussi calculer le paramètre de dispersion
disp <- s/(134-6-1)
disp## [1] 8.70632Dans ce cas la valeur de P est très petite (i.e. P est près de 0), le test de de Pearson nous permet donc de conclure que le modèle n’est pas adéquat pour ces données. Il s’agit probablement d’un problème de surdispersion puisque la somme des résiduels de Pearson divisée par les ddl est égale à 8.7 (ce qui est beaucoup plus grand que 1.25). La variance est donc > que la moyenne dans ce jeu de données.
8.1.8 Profils extrêmes ou influents
Comme pour la régression logistique, vous pouvez demander de créer une nouvelle table contenant, en plus de vos variables originales, les différentes valeurs (e.g. résiduels de Pearson, de Déviance, probabilité prédite, leviers) qui serviront à évaluer votre modèle. La fonction augment() du package broom vous permet de le faire. Vous pourrez ensuite trier cette table pour identifier, par exemple, les observations avec les résiduels, leviers ou distance de Cook les plus extrêmes et essayer de comprendre si ces observations ont quelque chose en commun.
library(broom)
diag <- augment(modele_incid) #Nous venons de créer une nouvelle table dans laquelle les résiduels, distance de cook, etc se trouvent maintenant
head(diag)## # A tibble: 6 × 11
## reactors type sex age offse…¹ .fitted .resid .std.…² .hat .sigma
## <int> <fct> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 boucherie femelle 0-12… 6.26 -4.98 2.83 2.83 0.00352 1.64
## 2 2 boucherie femelle 12-2… 8.21 -0.365 1.27 1.29 0.0247 1.66
## 3 5 boucherie femelle >24 … 8.66 0.0148 2.82 2.85 0.0168 1.64
## 4 3 boucherie mâle 12-2… 7.87 -1.06 2.77 2.80 0.0217 1.64
## 5 1 boucherie mâle >24 … 6.26 -2.74 1.90 1.91 0.00324 1.65
## 6 2 boucherie femelle >24 … 8.96 0.318 0.499 0.505 0.0228 1.66
## # … with 1 more variable: .cooksd <dbl>, and abbreviated variable names
## # ¹`offset(log_par)`, ².std.residNotez que les valeurs prédites sont sur une échelle de log(compte). Les valeurs prédites sur une échelle de compte par 1 animal-jour à risque ont cependant été conservées dans votre objet modèle. Vous pouvez donc simplement les ajouter à votre table de diagnostic, si vous le désirez. Vous pourriez aussi les multiplier par 100 000 pour avoir un taux par 100 000 animaux-jour (ou par 100 et par 365 pour un taux par 100 animaux-année).
diag$pred_count <- modele_incid$fitted.values
head(diag)## # A tibble: 6 × 12
## reactors type sex age offse…¹ .fitted .resid .std.…² .hat .sigma
## <int> <fct> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 boucherie femelle 0-12… 6.26 -4.98 2.83 2.83 0.00352 1.64
## 2 2 boucherie femelle 12-2… 8.21 -0.365 1.27 1.29 0.0247 1.66
## 3 5 boucherie femelle >24 … 8.66 0.0148 2.82 2.85 0.0168 1.64
## 4 3 boucherie mâle 12-2… 7.87 -1.06 2.77 2.80 0.0217 1.64
## 5 1 boucherie mâle >24 … 6.26 -2.74 1.90 1.91 0.00324 1.65
## 6 2 boucherie femelle >24 … 8.96 0.318 0.499 0.505 0.0228 1.66
## # … with 2 more variables: .cooksd <dbl>, pred_count <dbl>, and abbreviated
## # variable names ¹`offset(log_par)`, ².std.residÀ partir de cette table, vous pourriez produire les graphiques qui vous intéresseront à l’aide de la fonction ggplot() ou simplement classer la table pour voir les résiduels les plus grands, comme nous l’avons déjà fait précédemment.
8.1.9 Comparer les comptes observés et prédits
Vous pourrez représenter graphiquement les comptes observés vs. prédits de la manière suivante, en utilisant les résultats de votre modèle et la fonction ggplot() de la libraire ggplot2. Dans votre objet “modèle”, la variable y représente le compte observé d’évènements et la variable fitted.values représente le compte prédit d’évènements. Vous pouvez les mettre ensemble dans une même base de données et ensuite produire des histogrammes pour chacune de ces valeurs ou encore, comme à la figure 18.2 du livre VER, un polygone de fréquence.
#En premier, nous réunissons les valeurs observées et prédites dans un même jeu de données.
obs_pred <- data.frame(cbind(obs=modele_incid$y,
pred=modele_incid$fitted.values)
)
#Ensuite nous générons les deux polygones de fréquence dans une même figure.
library(ggplot2)
ggplot(data=obs_pred,
mapping=aes(x=obs)
) +
geom_freqpoly(color="blue") + #Nous demandons d'abord une ligne pour les valeurs observées
guides(color=FALSE) + #Nous demandons à ne pas avoir de légende dans ce cas
geom_freqpoly(mapping=aes(x=pred,
color="red")
) + #Nous demandons ensuite une ligne pour les valeurs prédites
xlim(0,
NA) + #Nous limitons l'axe à zéro
theme_bw() #Un thème blanc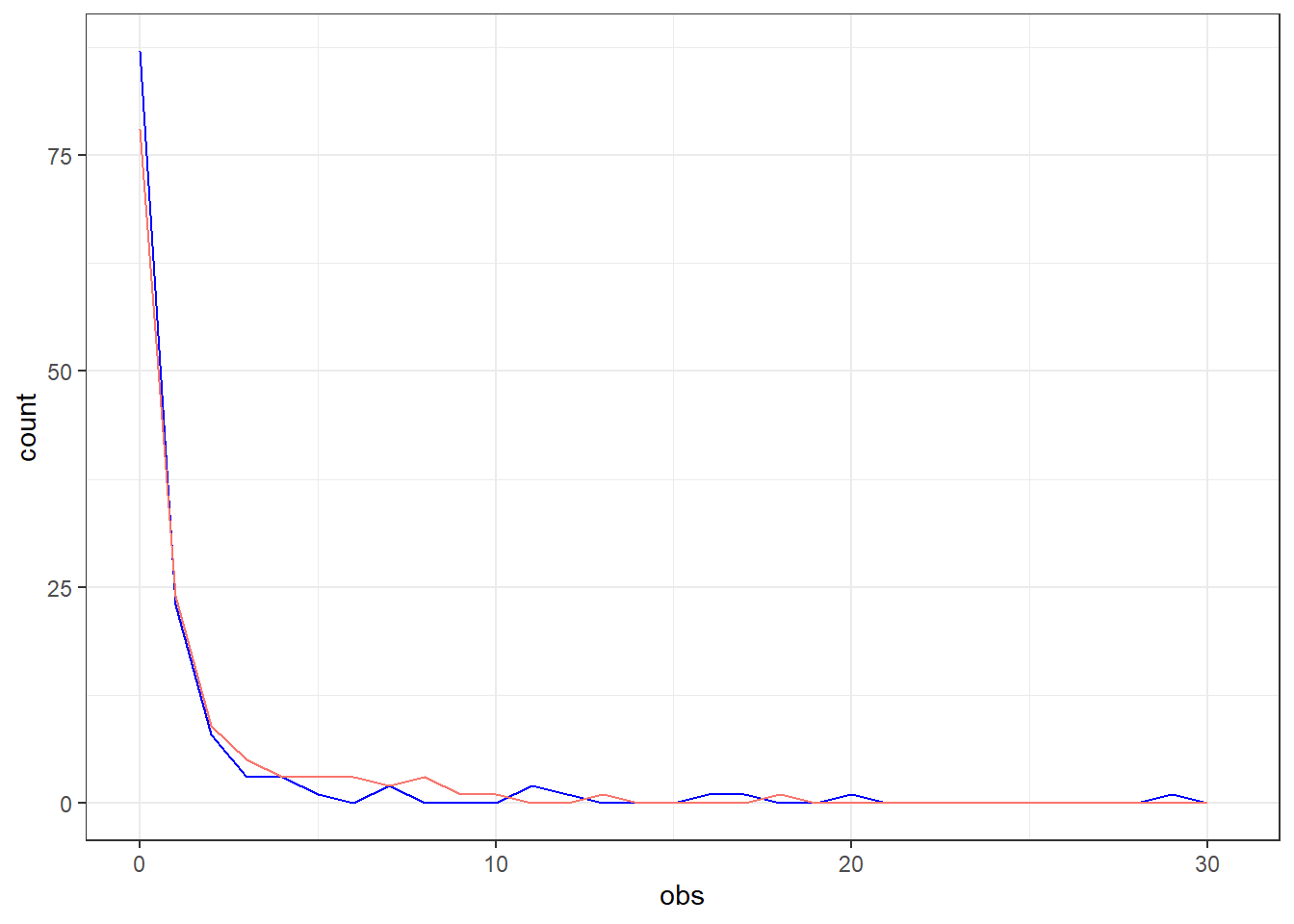
Figure 8.1: Comparaison des comptes d’animaux réactifs observés (bleu) et prédits (rouge).
Dans ce cas, on note un certain écart entre les comptes observés et prédits dans les troupeaux avec 0 animal positif (près de 87 troupeaux avaient 0 animal positif alors que le modèle prédit moins de troupeaux avec des comptes s’approchant de 0). Pour les autres valeurs, le modèle prédit des valeurs assez près des valeurs observées, mais est incapable de prédire des valeurs très élevées (e.g., 29 cas dans un troupeau).
8.1.10 Erreurs-type mises à l’échelle (scaled SE)
Une solution à la sur-dispersion est d’utiliser des erreurs-types mises à l’échelle (i.e. scaled SE). En fait, les erreurs-type sont alors simplement multipliées par la racine carrée du paramètre de dispersion de Pearson. Ce paramètre étant simplement la somme des résiduels de Pearson divisé par les degrés de liberté. En spécifiant family="quasipoisson" ce sera alors les erreurs-types mises à l’échelle qui vous seront présentées et qui serviront à calculer les IC95.
modele_scaled <- glm(data=tb,
reactors ~ type + sex + age + offset(log_par),
family="quasipoisson"
)
summary(modele_scaled)##
## Call:
## glm(formula = reactors ~ type + sex + age + offset(log_par),
## family = "quasipoisson", data = tb)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.5386 -0.8607 -0.3364 -0.0429 8.7903
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -11.6899 2.1828 -5.355 3.87e-07 ***
## typeboucherie 0.4422 0.6976 0.634 0.527
## typecervidé 1.0662 0.6886 1.548 0.124
## typeautre 0.4384 1.8144 0.242 0.809
## sexmâle -0.3619 0.5765 -0.628 0.531
## age12-24 mois 2.6734 2.1296 1.255 0.212
## age>24 mois 2.6012 2.1057 1.235 0.219
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 8.706329)
##
## Null deviance: 409.03 on 133 degrees of freedom
## Residual deviance: 348.35 on 127 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 8On note que les erreurs-types sont 2.9 fois plus grandes que ce qu’elles étaient avant. Notre facteur de dispersion était justement 8.7 et la racine carré de 8.7 est 2.9.
8.1.11 Variance robuste
Les erreurs-types robustes peuvent aussi être utilisées lorsqu’il y a problème de sur-dispersion (ou de nombreux autres problèmes comme la dépendance des données). La fonction sandwich() de la librairie sandwich permet de calculer la variance robuste pour le modèle, nous obtiendrons alors les erreurs-types robustes avec la racine carrée de ces variances.
library(sandwich)
#Nous demandons la variance robuste
rob_var<-sandwich(modele_incid)
#Les valeurs qui nous intéressent sont sur la diagonale, la fonction diag nous permet de les isoler
rob_var<-diag(rob_var)
#Et maintenant nous appliquons la racine carrée
rob_SE <- sqrt(rob_var)
#Vous auriez aussi pu faire:
#rob_SE <-sqrt(diag(sandwich(modele_incid)))
#Pour faciliter la lecture, nous pourrions ajouter ces erreurs-types robustes à nos coefficients dans une même table
tab_SE <- data.frame(cbind(Estimate=modele_incid$coefficients,
robust_SE=rob_SE)
)
library(knitr)
library(kableExtra)
kable(round(tab_SE,
digits=3),
caption="Modèle de Poisson avec erreurs-types robustes.")%>%
kable_styling()| Estimate | robust_SE | |
|---|---|---|
| (Intercept) | -11.690 | 0.913 |
| typeboucherie | 0.442 | 0.456 |
| typecervidé | 1.066 | 0.496 |
| typeautre | 0.438 | 0.764 |
| sexmâle | -0.362 | 0.432 |
| age12-24 mois | 2.673 | 0.858 |
| age>24 mois | 2.601 | 0.854 |
Notez que, si vous désirez utiliser des erreurs-types robustes ET les intégrer dans un ajustement pour comparaisons multiples, c’est un peu plus compliqué. Vous devrez combiner la librairie multcomp et la librairie sandwich. Nous utilisons la fonction glht() de cette première librairie pour obtenir des comparaisons multiples et l’option vcov=sandwichpour utiliser la variance robuste.
library(multcomp)
library(sandwich)
#Ici nous demandons une comparaison multiple avec ajustement de Tukey et les erreur-types robustes
tukey <- glht(modele_incid,
linfct = mcp(type="Tukey",
age="Tukey",
sex="Tukey"),
vcov = sandwich)
#Nous ajoutons les IC95
with_ci <- confint(tukey)
#Nous les transformons en IR
tukey_results <- exp(with_ci$confint)
#Nous présentons la table en arrondissant les IR à 2 décimales.
library(knitr)
library(kableExtra)
kable(round(tukey_results,
digits=2),
caption="IR du modèle de Poisson avec erreur-types robustes et IC95 ajustées pour comparaisons multiples.")%>%
kable_styling()| Estimate | lwr | upr | |
|---|---|---|---|
| type: boucherie - laitier | 1.56 | 0.45 | 5.40 |
| type: cervidé - laitier | 2.90 | 0.75 | 11.27 |
| type: autre - laitier | 1.55 | 0.19 | 12.52 |
| type: cervidé - boucherie | 1.87 | 0.49 | 7.11 |
| type: autre - boucherie | 1.00 | 0.12 | 8.40 |
| type: autre - cervidé | 0.53 | 0.07 | 4.26 |
| age: 12-24 mois - 0-12 mois | 14.49 | 1.39 | 151.20 |
| age: >24 mois - 0-12 mois | 13.48 | 1.31 | 139.14 |
| age: >24 mois - 12-24 mois | 0.93 | 0.31 | 2.82 |
| sex: mâle - femelle | 0.70 | 0.21 | 2.27 |
8.2 Régression binomiale négative
Pour effectuer une régression binomiale négative, vous devez utiliser la fonction glm.nb() de la librairie MASS comme suit.
library(MASS)
modele_nb <- glm.nb(data=tb,
reactors ~ type + sex + age + offset(log_par)
)
summary(modele_nb)##
## Call:
## glm.nb(formula = reactors ~ type + sex + age + offset(log_par),
## data = tb, init.theta = 0.5745887328, link = log)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.77667 -0.74441 -0.45509 -0.09632 2.70012
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -11.18145 0.92302 -12.114 < 2e-16 ***
## typeboucherie 0.60461 0.62282 0.971 0.331665
## typecervidé 0.66572 0.63176 1.054 0.291993
## typeautre 0.80003 0.96988 0.825 0.409442
## sexmâle -0.05748 0.38337 -0.150 0.880819
## age12-24 mois 2.25304 0.77915 2.892 0.003832 **
## age>24 mois 2.48095 0.75283 3.296 0.000982 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(0.5746) family taken to be 1)
##
## Null deviance: 111.33 on 133 degrees of freedom
## Residual deviance: 99.36 on 127 degrees of freedom
## AIC: 331.47
##
## Number of Fisher Scoring iterations: 1
##
##
## Theta: 0.575
## Std. Err.: 0.143
##
## 2 x log-likelihood: -315.472Le paramètre de dispersion (Theta) et son erreur-type sont rapportés en bas.
8.2.1 Comparer les modèles Poisson et Binomial négatif
Un test de rapport de vraisemblance peut être utilisé pour vérifier si l’ajout du facteur de dispersion est statistiquement significatif (i.e., pour vérifier si le modèle Binomial négatif est statistiquement meilleur que le Poisson).
library(lmtest)
lrtest(modele_incid,
modele_nb)## Likelihood ratio test
##
## Model 1: reactors ~ type + sex + age + offset(log_par)
## Model 2: reactors ~ type + sex + age + offset(log_par)
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 7 -238.66
## 2 8 -157.74 1 161.85 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Dans ce cas, on note que l’ajout du facteur de dispersion est statistiquement significatif (P < 0.001).
8.2.2 Évaluer les résiduels d’un modèle Binomial négatif
Malheureusement, la librairie broom que nous avons utilisée jusqu’à présent pour générer une table de diagnostic ne fonctionne plus avec le modèle Binomial négatif estimé avec la fonction glm.nb() de la librairie MASS. Ces résiduels peuvent cependant être générés avec la fonction simulateResiduals() de la librairieDHARMa.
library(DHARMa)
#Permet de générer des résiduels par simulation
negbin_simulation <- simulateResiduals(fittedModel = modele_nb)
#Permet de visualiser les résiduels vs les valeurs prédites.
plotSimulatedResiduals(simulationOutput = negbin_simulation)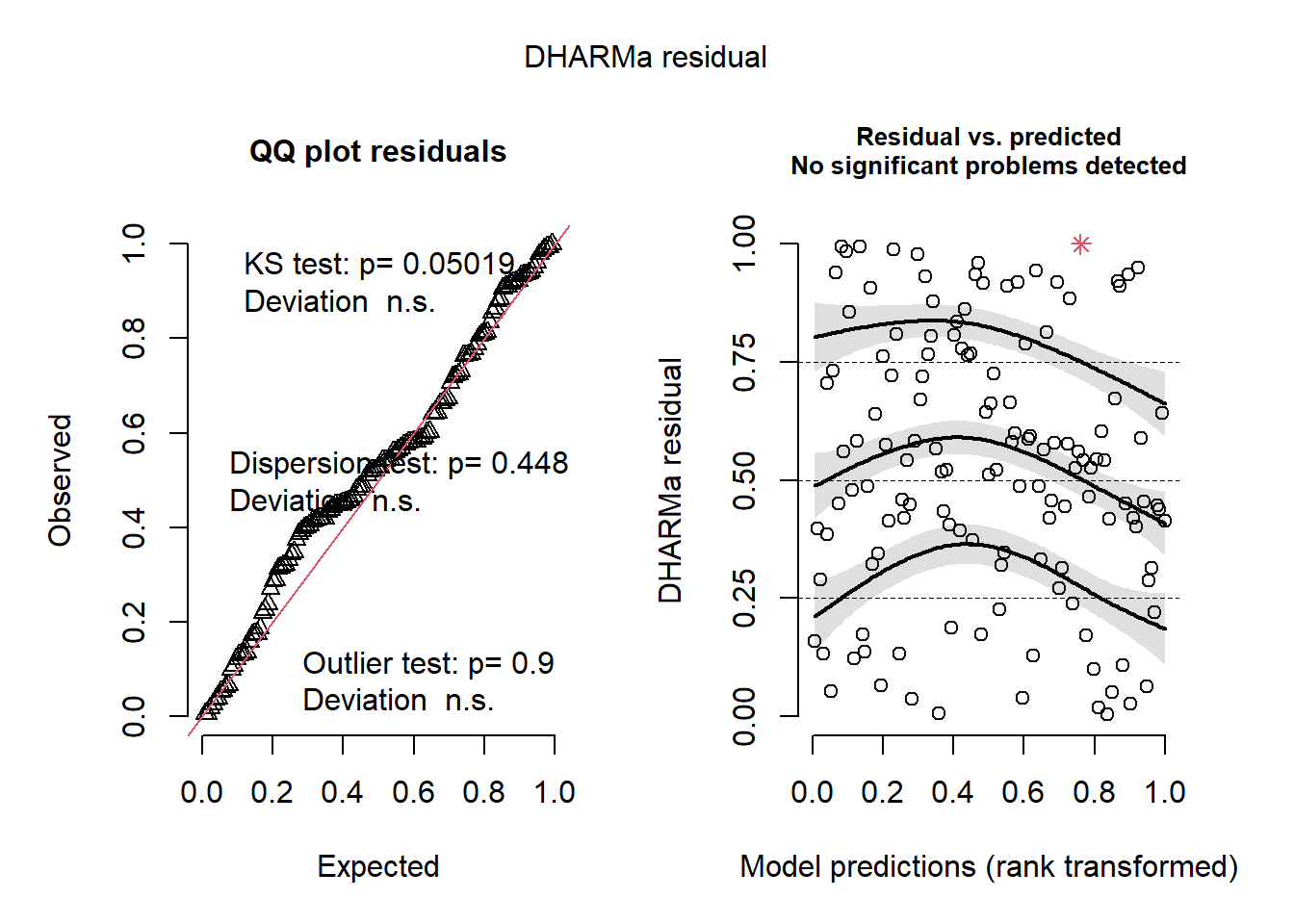
#Tester avec le Pearson chi-square test s'il y a surdispersion
testDispersion(negbin_simulation, type="PearsonChisq")##
## Parametric dispersion test via mean Pearson-chisq statistic
##
## data: negbin_simulation
## dispersion = 2.9516, df = 127, p-value < 2.2e-16
## alternative hypothesis: two.sidedDans ce cas, il semble y avoir encore une très légère surdispersion (Pearson/DDL=2.95 > 1.25)…
8.3 Modèles zéro-enflés
8.3.1 Généralités
Parfois le nombre de zéros est plus grand ou plus petit que ce que l’on attend avec une distribution de Poisson ou Binomiale négative. On peut alors avoir recours à un modèle pour excès de zéros (un modèle zéros-enflés de Poisson ou zéros-enflés Binomial négatif, respectivement abréviés ZIP ou ZINB) ou le modèle à barrière (hurdle model). S’il n’y a pas de zéros, on peut alors utiliser un modèle à zéros tronqués (zero-truncated model) ou simplement soustraire la valeur 1 de notre variable dépendante.
Pour cette section, nous travaillerons avec la base de données fec.csv. Celle-ci décrit le nombre d’oeufs de parasite/5g de fèces en fonction de différents prédicteurs. Dans cet exemple, il n’y a pas de dénominateur à prendre en compte (i.e. pas de variable offset).
#Nous importons la base de données
fec <-read.csv(file="fec.csv",
header=TRUE,
sep=";"
)
#Nous recodons certaines variables
fec$fec<-as.numeric(fec$fec)
fec$lact<-as.factor(fec$lact)
fec$past_lact<-as.factor(fec$past_lact)
fec$man_heif<-as.factor(fec$man_heif)
fec$man_lact<-as.factor(fec$man_lact)
#Visualisons la base de données
head(fec)## province herd cow visit tx fec lact season past_lact man_heif man_lact
## 1 1 1 46 5 0 3 1 2 1 0 0
## 2 1 1 46 6 0 3 1 2 1 0 0
## 3 1 1 46 7 0 11 1 2 1 0 0
## 4 1 1 46 8 0 7 1 3 1 0 0
## 5 1 1 46 9 0 17 1 3 1 0 0
## 6 1 1 46 10 0 6 1 3 1 0 0#Distribution de notre variable dépendante (fec)
library(ggplot2)
ggplot(fec,
aes(x=fec)
) +
geom_histogram(colour="black",
fill="grey") +
theme_bw() +
xlab("Nombre d'oeufs/5g de fèces") +
ylab("Nombre de vaches")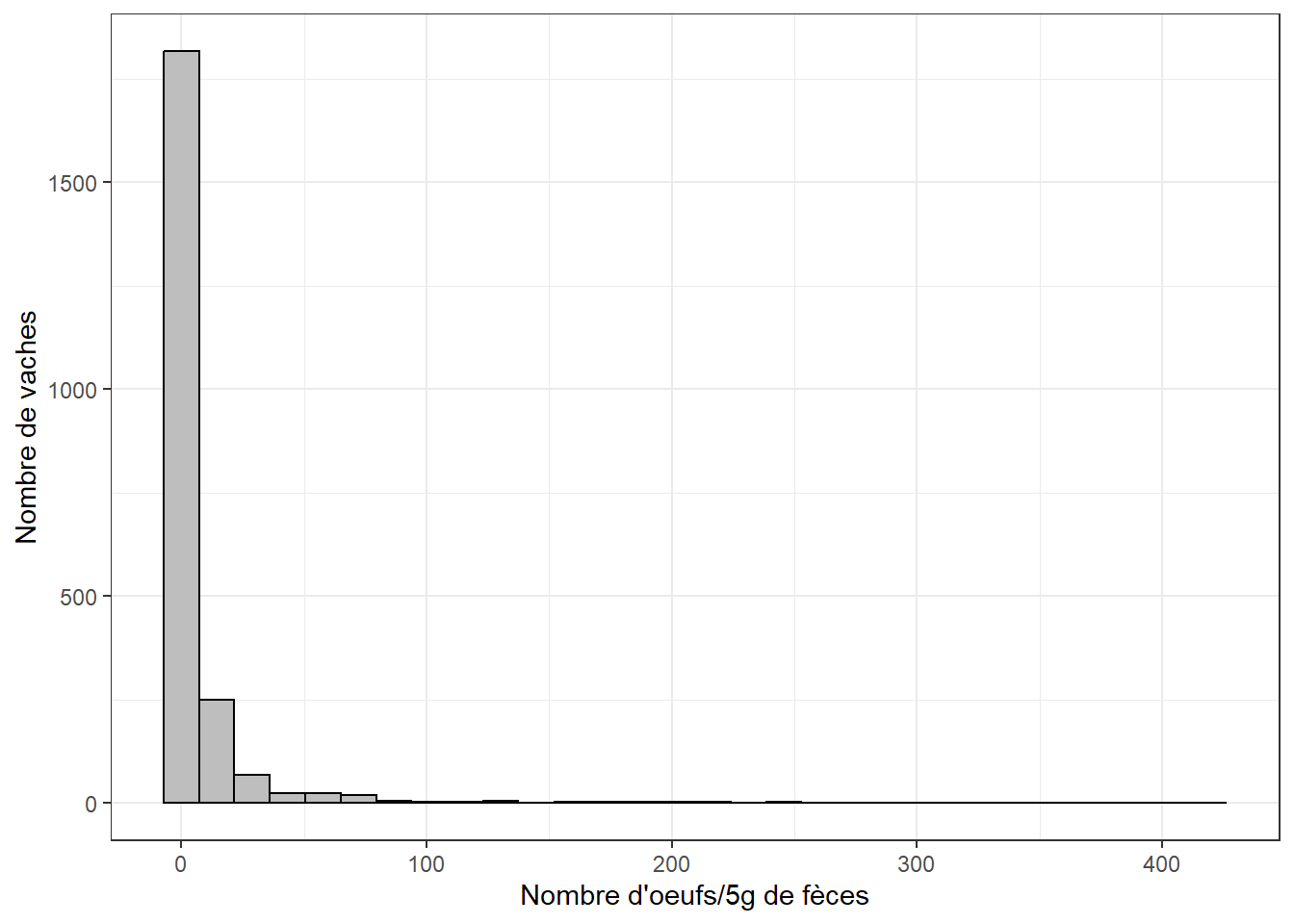
On note une distribution qui s’étire vers la droite et avec beaucoup de vaches avec la valeur zéro.
La fonction zeroinfl() de la librairie pscl permettra de générer les modèles zéros-enflés de Poisson ou Binomial négatif. Les modèles pour excès de zéros travaillent en appliquant simultanément une régression logistique et une régression de Poisson (ou Binomiale négative). Les deux parties du modèle peuvent avoir les mêmes prédicteurs, mais ce n’est pas obligatoire. Notez que la partie logistique du modèle prédit la probabilité d’avoir un compte de zéro (et donc les coefficients ont un signe opposé à ce qu’ils auraient dans une régression logistique « conventionnelle », où les “1” seraient prédits).
Le code suivant permet d’évaluer un modèle zéros-enflés Binomial négatif évaluant l’effet de différents prédicteurs (lact= multipare, past_lac= accès au pâturage, man_heif= fumier étendu sur pâturage des taures, man_lac=fumier étendu sur pâturage des vaches adultes) sur le compte d’œufs de parasites/5g de fèces.
library(pscl)
modele_zinb <- zeroinfl(data=fec,
fec ~ lact + past_lact + man_heif + man_lact,
dist="negbin"
)
summary(modele_zinb)##
## Call:
## zeroinfl(formula = fec ~ lact + past_lact + man_heif + man_lact, data = fec,
## dist = "negbin")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -0.5055 -0.4537 -0.3624 -0.1425 27.3062
##
## Count model coefficients (negbin with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.36949 0.13117 18.064 < 2e-16 ***
## lact1 -1.15848 0.10664 -10.864 < 2e-16 ***
## past_lact1 0.53667 0.14233 3.771 0.000163 ***
## man_heif1 -0.99846 0.14216 -7.023 2.16e-12 ***
## man_lact1 1.07856 0.15789 6.831 8.43e-12 ***
## Log(theta) -1.35981 0.05425 -25.065 < 2e-16 ***
##
## Zero-inflation model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.9303 0.2932 -3.173 0.00151 **
## lact1 0.8700 0.3083 2.822 0.00478 **
## past_lact1 -1.8003 0.3990 -4.512 6.41e-06 ***
## man_heif1 -0.7701 0.4669 -1.649 0.09905 .
## man_lact1 -12.0963 156.4271 -0.077 0.93836
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Theta = 0.2567
## Number of iterations in BFGS optimization: 47
## Log-likelihood: -5239 on 11 DfNotez que les résultats présentés sont passablement différents. Vous avez deux tables avec les estimés des paramètres, une (Count model coefficients) pour la partie binomiale négative (i.e. les comptes) et l’autre (Zero-inflation model coefficients) pour la partie zéros-enflés (i.e. la partie logistique ou, si vous préférez, l’excès de zéros).
On pourrait ajouter nos IC95 et mettre nos coefficients à l’exposant pour mieux visualiser les résultats. Notez que la librairie jtools (qui faisait automatiquement de jolies tables de résultats) ne fonctionne pas avec ce genre de modèle. Dommage…
# LA PARTIE LOGISTIQUE
# Extraire les coefficients et les erreurs types de la partie logistique (binomiale) du modèle dans une même table
coefs_logi <- as.data.frame(summary(modele_zinb)$coefficients$zero[,1:2])
names(coefs_logi)[2] = "SE"
# Calculer les IC95
coefs_logi$lower.ci <- coefs_logi$Estimate-1.96*coefs_logi$SE
coefs_logi$upper.ci <- coefs_logi$Estimate+1.96*coefs_logi$SE
#Ici on pourrait déjà, si on le voulait, inverser tous les coefficients et les CI
# Mettre à l'exposant les coefficients
OR <- exp(coefs_logi)
# Retirer l'intercept (la 1ère rangée) et les erreurs-types
OR <- OR[-c(1), ]
OR <- subset(OR, select = -c(SE))
# LA PARTIE COMPTE
# Extraire les coefficients et les erreurs types de la partie Binomiale négative du modèle dans une même table
coefs <- as.data.frame(summary(modele_zinb)$coefficients$count[,1:2])
names(coefs)[2] = "SE"
# Calculer les IC95
coefs$lower.ci <- coefs$Estimate-1.96*coefs$SE
coefs$upper.ci <- coefs$Estimate+1.96*coefs$SE
# Mettre à l'exposant les coefficients
IR <- exp(coefs)
# Retirer l'intercept (la 1ère rangée), le paramètre de dispersion (la 6ième rangée) et les erreurs-types
IR <- IR[-c(1, 6), ]
IR <- subset(IR, select=-c(SE))
#Finalement, on pourra demander à voir ces tables
library(knitr)
library(kableExtra)
kable(round(OR, digits=2), caption="Partie logistique du modèle zéro-enflé Binomial négatif (ZINB).")%>%
kable_styling()| Estimate | lower.ci | upper.ci | |
|---|---|---|---|
| lact1 | 2.39 | 1.30 | 4.370000e+00 |
| past_lact1 | 0.17 | 0.08 | 3.600000e-01 |
| man_heif1 | 0.46 | 0.19 | 1.160000e+00 |
| man_lact1 | 0.00 | 0.00 | 7.945616e+127 |
kable(round(IR, digits=2), caption="Partie binomiale négative du modèle zéro-enflé Binomial négatif (ZINB).")%>%
kable_styling()| Estimate | lower.ci | upper.ci | |
|---|---|---|---|
| lact1 | 0.31 | 0.25 | 0.39 |
| past_lact1 | 1.71 | 1.29 | 2.26 |
| man_heif1 | 0.37 | 0.28 | 0.49 |
| man_lact1 | 2.94 | 2.16 | 4.01 |
L’interprétation des coefficients de régression, par exemple pour la variable lact (primipare=0 est la valeur de référence et multipare=1) se fera comme suit : Les vaches multipares avaient 2.4 fois (IC95: 1.3, 4.4) les odds d’avoir aucun œufs de parasites dans leurs fèces comparativement aux primipares et elles avaient 0.31 fois (IC95: 0.25, 0.39) le compte d’œufs de parasites des primipares.
Bien sûr, vous pouvez encore utiliser certaines fonctions que vous avez maintenant l’habitude d’utiliser, par exemple les fonctions emmeans() et pairs() du package emmeans .
8.3.2 Test de Vuong – Comparer modèle zéros-enflés au modèle conventionnel
On peut vérifier si un modèle pour excès de zéros est plus approprié que le modèle de Poisson ou Binomial négatif équivalent grâce au test de Vuong. Pour ce faire, on devra d’abord générer un objet modèle Poisson et un autre objet modèle zéro-enflé Poisson (ou un Binomial négatif et un zéro-enflé Binomial négatif). Ensuite, la fonction vuong() de la librairie pscl permettra de comparer ces modèles.
# Le modèle NB
library(MASS)
modele_nb <- glm.nb(data=fec,
fec ~ lact + past_lact + man_heif + man_lact
)
# Le modèle ZINB
library(pscl)
modele_zinb <- zeroinfl(data=fec,
fec ~ lact + past_lact + man_heif + man_lact,
dist="negbin"
)
#Le test de Vuong
vuong(modele_nb,
modele_zinb)## Vuong Non-Nested Hypothesis Test-Statistic:
## (test-statistic is asymptotically distributed N(0,1) under the
## null that the models are indistinguishible)
## -------------------------------------------------------------
## Vuong z-statistic H_A p-value
## Raw -3.3087359 model2 > model1 0.00046859
## AIC-corrected -2.6889996 model2 > model1 0.00358332
## BIC-corrected -0.9169612 model2 > model1 0.17958149Trois tests statistiques différents sont réalisés. Dans tous les cas le modèle zéros-enflés (le #2) semble préférable et deux de ces tests indiquent une différence statistiquement significative entre les modèles ZINB et NB.
8.4 Calcul du risque relatif à l’aide d’une régression de Poisson
Avec une variable dépendante qui ne peut prendre que 2 valeurs (0/1), on utilise en général la régression logistique et ont présente donc un rapport de cotes (i.e. un odds ratio). Dans certaines situations, cependant, on préfèrerait présenter un risque relatif plutôt qu’un rapport de cotes. Par exemple, pour faciliter la compréhension des résultats (i.e. le risque relatif est plus facile à comprendre que le rapport de cotes) ou pour permettre le calcul d’autres mesures d’association (e.g. la fraction attribuable dans la population).
Si la maladie est rare (prévalence < 5%), le rapport de cotes ≈ le risque relatif. Mais si la maladie est relativement fréquente, on ne pourra se servir de cette particularité. On peut, cependant, utiliser une régression de Poisson et un lien log avec une variable dépendante binaire. L’exposant des coefficients sera alors un risque relatif (plutôt qu’un rapport de cotes). Les IC 95% seront, cependant, un peu trop conservateurs (i.e. trop larges). On pourra y remédier en utilisant des erreurs-types robustes. Voir (Barros et Hirakata, 2003.6 pour plus de détails.
Le code suivant permet de calculer des risques relatifs (plutôt que des rapports de cotes) pour le risque de Nocardiose en fonction des traitements au tarissement utilisés.
#Nous importons le jeu de données
nocardia <-read.csv(file="nocardia.csv",
header=TRUE,
sep=";"
)
#Nous indiquons les variables catégoriques dans le jeu de données
nocardia$dbarn <- factor(nocardia$dbarn)
nocardia$dneo <- factor(nocardia$dneo)
nocardia$dclox <- factor(nocardia$dclox)
#Nous effectuons une régression de Poisson
modele_poisson <- glm(data=nocardia,
casecont ~ dclox + dneo + dcpct, family="poisson"
)
#Nous demandons la variance robuste
library(sandwich)
rob_SE <-sqrt(diag(sandwich(modele_poisson)))
#Pour faciliter la lecture, nous pourrions ajouter ces erreurs-types robustes à nos coefficients dans une table
tab_SE <- data.frame(cbind(Estimate=modele_poisson$coefficients,
robust_SE=rob_SE)
)
#Puis calculer les IC95
tab_SE$lower.ci <- tab_SE$Estimate-1.96*tab_SE$robust_SE
tab_SE$upper.ci <- tab_SE$Estimate+1.96*tab_SE$robust_SE
#Enlever l'intercept, les SE et mettre tout à l'exposant pour avoir des RR
tab_SE <- tab_SE[-c(1), ]
tab_SE <- exp(subset(tab_SE,
select=-c(robust_SE)
)
)
library(knitr)
library(kableExtra)
kable(round(tab_SE, digits=2),
caption="Modèle de Poisson avec erreurs-types robustes pour estimer le risque relatif de Nocardiose.")%>%
kable_styling()| Estimate | lower.ci | upper.ci | |
|---|---|---|---|
| dclox1 | 0.56 | 0.31 | 1.02 |
| dneo1 | 3.56 | 1.55 | 8.14 |
| dcpct | 1.01 | 1.00 | 1.02 |
Le risque relatif (RR) de Nocardiose dans les troupeaux utilisant la néomycine (vs. ceux qui ne l’utilisaient pas) était est donc de 3.56 (IC95: 1.55, 8.14).
8.5 Travaux pratiques 6 - Régression de Poisson et Binomiale négative
8.5.1 Exercices
Pour ce TP utilisez le fichier TB_real (voir description VER p.836).
Dans cette étude nous sommes intéressés à décrire les facteurs de risque associés à l’incidence d’animaux positifs à la tuberculose. L’incidence est définie à l’aide des variables reactors (le nombre d’animaux positif sur une ferme) et par (le nombre d’animal-jour à risque sur cette ferme).
Quel genre de valeurs la variable reactors prend-t’elle? Évaluer graphiquement la distribution de la variable reactors. Quel genre de distribution la variable reactors semble-t-elle suivre ? Justifiez.
Évaluez graphiquement la distribution du nombre d’animal-jour à risque (variable par). Y-a-t-il beaucoup de variation d’une ferme à l’autre ? Comment pourrez-vous tenir compte de ces différences dans un modèle de régression de Poisson ?
Évaluer l’effet du type d’élevage (i.e. la variable type) sur l’incidence d’animaux positifs à la tuberculose (reactors) tout en prenant en compte les nombres différents d’animal-jour à risque dans chacune des fermes.
3.1. Est-ce que la variable type est significativement associée à l’incidence de tuberculose (i.e. est-ce qu’au moins un des coefficients de régression des variables indicateurs est différent de zéro)?
3.2. Quels sont les ratios d’incidence, leurs IC 95% et les valeurs de P pour chacun des types d’élevage (utilisez laitier comme valeur de référence)?
3.3. Comment interprétez-vous le ratio d’incidence des cervidés?
3.4. Bien certainement, vous vous rappelez que vous devez ajuster ces IC 95% et valeurs de P pour les comparaisons multiples… Effectuez cet ajustement à l’aide de la méthode Tukey-Kramer. Les IC 95% et valeurs de P sont-elles maintenant plus grandes ou plus petites?
3.5. Est-ce que ce modèle semble adéquat pour ces données?
3.6. Y-a-t-il sur-dispersion? Si c’est le cas, quelles options avez-vous afin d’améliorer votre modèle?
3.7. Évaluez les ratios d’incidence, leurs IC 95% et les valeurs de P pour chacun des types d’élevage, mais à l’aide des erreurs-types robustes et en ajustant pour les comparaisons multiples. Est-ce que la variable type est toujours significativement associée à l’incidence de tuberculose (i.e. est-ce qu’au moins un des coefficients de régression des variables indicateurs est différent de zéro)?
3.8. Un modèle de régression binomiale négative permettrait peut-être de modéliser correctement cette sur-dispersion. Évaluez un tel modèle. Est-ce que le paramètre de dispersion semble significativement différent de zéro? Effectuez un test de rapport de vraisemblance comparant les modèles de régression binomial négative et de Poisson.
3.9. Comparez graphiquement le compte d’animaux positifs à la tuberculose prédits par ce dernier modèle et les comptes réels d’animaux positifs. Que notez-vous?
8.5.2 Code R et réponses
Pour ce TP utilisez le fichier TB_real (voir description VER p.836).
#Nous importons le jeu de données
tb <-read.csv(file="tb_real.csv",
header=TRUE,
sep=";")
head(tb)## obs farm_id type sex age reactors par
## 1 1 4002 2 0 0 1 525
## 2 2 4002 2 0 1 2 3675
## 3 3 4002 2 0 2 5 5775
## 4 4 4002 2 1 1 3 2625
## 5 5 4002 2 1 2 1 525
## 6 6 4003 2 0 2 2 7824#Nous indiquons les variables catégoriques dans le jeu de données. Nous allons aussi ajouter des étiquettes pour faciliter l'interprétation plus tard.
tb$farm_id <- factor(tb$farm_id)
tb$type <- factor(tb$type,
levels=c(1,2,3,4),
labels=c("laitier",
"boucherie",
"cervidé",
"autre")
)
tb$sex <- factor(tb$sex,
levels=c(0,1),
labels=c("femelle",
"mâle")
)
tb$age <- factor(tb$age,
levels=c(0:2),
labels=c("0-12 mois",
"12-24 mois",
">24 mois")
)Dans cette étude nous sommes intéressés à décrire les facteurs de risque associés à l’incidence d’animaux positifs à la tuberculose. L’incidence est définie à l’aide des variables reactors (le nombre d’animaux positif sur une ferme) et par (le nombre d’animal-jour à risque sur cette ferme).
- Quel genre de valeurs la variable reactors prend-t’elle? Évaluer graphiquement la distribution de la variable reactors. Quel genre de distribution la variable reactors semble-t-elle suivre ? Justifiez.
library(summarytools)
print(dfSummary(tb$reactors),
method='render')Data Frame Summary
tb
Dimensions: 134 x 1Duplicates: 121
| No | Variable | Stats / Values | Freqs (% of Valid) | Graph | Valid | Missing | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | tb [integer] |
|
13 distinct values | 134 (100.0%) | 0 (0.0%) |
Generated by summarytools 1.0.1 (R version 4.2.0)
2023-01-19
Réponse: reactors ne prend que des valeurs entières positives (0, 1, 2, 3, …). reactors représente des données de comptes et semble suivre une distribution de Poisson: -les données de petite valeur sont fréquentes (0, 1, 2), -à partir d’une certaine valeur, la fréquence décroît rapidement,
- Évaluez graphiquement la distribution du nombre d’animal-jour à risque (variable par). Y-a-t-il beaucoup de variation d’une ferme à l’autre ? Comment pourrez-vous tenir compte de ces différences dans un modèle de régression de Poisson ?
library(summarytools)
print(dfSummary(tb$par),
method='render')Data Frame Summary
tb
Dimensions: 134 x 1Duplicates: 14
| No | Variable | Stats / Values | Freqs (% of Valid) | Graph | Valid | Missing | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | tb [numeric] |
|
120 distinct values | 134 (100.0%) | 0 (0.0%) |
Generated by summarytools 1.0.1 (R version 4.2.0)
2023-01-19
Réponse: Oui, beaucoup de fermes ont peu d’animal-jour à risque (i.e. elles comptaient peu d’animaux et/ou elles avaient été suivies pendant peu de jours) alors que d’autres ont des valeurs de par élevées. Ces différences pourraient être gérées dans une régression de Poisson en spécifiant une variable offset qui sera en fait le logarithme naturel de par.
- Évaluer l’effet du type d’élevage (i.e. la variable type) sur l’incidence d’animaux positifs à la tuberculose (reactors) tout en prenant en compte les nombres différents d’animal-jour à risque dans chacune des fermes.
#Nous devons d'abord créer un offset en transformant la variable "par" sur une échelle logarithmique
tb$log_par <- log(tb$par)
#Ensuite nous générons un objet modèle, pour une régression de Poisson, le prédicteur "type" et le offset "log_par"
modele_incid<-glm(data=tb,
reactors ~ type + offset(log_par),
family="poisson"
)3.1. Est-ce que la variable type est significativement associée à l’incidence de tuberculose (i.e. est-ce qu’au moins un des coefficients de régression des variables indicatrices est différent de zéro)?
summary(modele_incid)##
## Call:
## glm(formula = reactors ~ type + offset(log_par), family = "poisson",
## data = tb)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.7137 -1.1568 -0.4825 -0.1190 9.0537
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -9.1000 0.2000 -45.500 < 2e-16 ***
## typeboucherie 0.3294 0.2353 1.400 0.161603
## typecervidé 0.8122 0.2232 3.639 0.000273 ***
## typeautre 0.3063 0.6110 0.501 0.616102
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 409.03 on 133 degrees of freedom
## Residual deviance: 390.50 on 130 degrees of freedom
## AIC: 527.47
##
## Number of Fisher Scoring iterations: 6Réponse: Ici ont voit que cervidés semble différent de la valeur de référence (laitier). Mais ce serait préférable de faire un test de rapport de vraisemblance sur l’ensemble des variables indicateurs.
library(lmtest)
lrtest(modele_incid) #test du rapport de vraisemblance du modèle## Likelihood ratio test
##
## Model 1: reactors ~ type + offset(log_par)
## Model 2: reactors ~ 1
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 4 -259.74
## 2 1 -396.90 -3 274.32 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Réponse: Le test de rapport de vraisemblance comparant le modèle avec la variable type et sans celle-ci est significatif (P<0.001).
3.2. Quels sont les ratios d’incidence et leurs IC 95% pour chacun des types d’élevage (utilisez laitier comme valeur de référence)?
#Comme laitier est déjà la valeur de référence, nous pouvons simplement faire:
library(jtools)
#Nous utilisons la librairie jtools pour obtenir une table avec les coefficients et les IC95
j <- summ(modele_incid,
confint = TRUE)
#Nous utilisons round pour ajuster la précision des valeurs dans les tables
round(exp(j$coeftable),
digits=2)## Est. 2.5% 97.5% z val. p
## (Intercept) 0.00 0.00 0.00 0.00 1.00
## typeboucherie 1.39 0.88 2.20 4.05 1.18
## typecervidé 2.25 1.45 3.49 38.07 1.00
## typeautre 1.36 0.41 4.50 1.65 1.85Réponse: Pour ce calcul, on aurait aussi pu simplement faire l’exposant des coefficients et des IC 95% rapportés à l’aide de ma fonction summary().
3.3. Comment interprétez-vous le ratio d’incidence des cervidés?
Réponse: L’incidence de tuberculose est 2.25 fois plus élevée (IC95: 1.45, 3.49) dans les élevages de cervidés comparativement aux élevages laitiers.
3.4. Bien certainement, vous vous rappelez que vous devez ajuster ces IC 95% et valeurs de P pour les comparaisons multiples… Effectuez cet ajustement à l’aide de la méthode Tukey-Kramer. Les IC 95% sont-elles maintenant plus grands ou plus petits?
library(emmeans)
contrast <- emmeans(modele_incid,
c("type"))
#Notez ici, nous avons ajouté l'option "reverse=TRUE" pour présenter les comparaisons dans l'autre sens (i.e., comme dans le summary()).
confint(pairs(contrast,
reverse = TRUE,
type="response")
)## contrast ratio SE df asymp.LCL asymp.UCL
## boucherie / laitier 1.390 0.327 Inf 0.759 2.54
## cervidé / laitier 2.253 0.503 Inf 1.270 4.00
## cervidé / boucherie 1.621 0.257 Inf 1.078 2.44
## autre / laitier 1.358 0.830 Inf 0.283 6.53
## autre / boucherie 0.977 0.577 Inf 0.214 4.45
## autre / cervidé 0.603 0.353 Inf 0.134 2.72
##
## Confidence level used: 0.95
## Conf-level adjustment: tukey method for comparing a family of 4 estimates
## Intervals are back-transformed from the log scaleRéponse: Bien évidemment les IC 95% sont plus larges (par exemple 1.27, 4.0 après ajustement pour les comparaisons multiples vs. 1.45, 3.49).
3.5. Est-ce que ce modèle semble adéquat pour ces données?
library(broom)
diag <- augment(modele_incid,
type.residuals = "pearson") #Nous venons de créer une nouvelle table avec les résiduels, etc.
#Nous calculons la somme de ces résiduels au carré. Dans ce cas: 791.0
s <- sum(diag$.resid^2)
s## [1] 791.0448#Nous vérifions à quelle probabilité la valeur 791.0 correspond dans une distribution de chi-carré avec les degrés de liberté (n - le nombre de coefficients-1).
P <- 1-pchisq(s,
(134-3-1))
P## [1] 0Réponse: Le test de de Pearson donne une valeur de P < 0.001, l’hypothèse nulle doit donc être rejetée, le modèle n’est pas adéquat pour les données.
3.6. Y-a-t-il sur-dispersion? Si c’est le cas, quelles options avez-vous afin d’améliorer votre modèle?
#Nous pouvons calculer le paramètre de dispersion
disp <- s/(134-3-1)
disp## [1] 6.08496Réponse: La somme des résiduels de Pearson/ddl = 6.08, il y a donc surdispersion (i.e. >1.25). Plusieurs options permettraient de contrôler ce problème, entre autres l’utilisation d’erreurs-type « scaled » ou robustes ou l’utilisation d’un modèle de régression binomiale négative.
3.7. Évaluez les ratios d’incidence, leurs IC 95% et les valeurs de P pour chacun des types d’élevage, mais à l’aide des erreurs-types robustes et en ajustant pour les comparaisons multiples. Est-ce que la variable type est toujours significativement associée à l’incidence de tuberculose (i.e. est-ce qu’au moins un des coefficients de régression des variables indicateurs est différent de zéro)?
library(multcomp)
library(sandwich)
#Ici nous demandons les comparaisons avec ajustement de Tukey et les erreurs-types robustes
tukey <- glht(modele_incid,
linfct = mcp(type="Tukey"),
vcov = sandwich)
#On ajoute les IC95
with_ci <- confint(tukey)
#On les transforme en IR
tukey_results <- exp(with_ci$confint)
#On présente la table en arrondissant les IR à 2 décimales.
library(knitr)
library(kableExtra)
kable(round(tukey_results, digits=2),
caption="IR du modèle de Poisson avec erreurs-types robustes et IC95 ajustées pour comparaisons multiples.")%>%
kable_styling()| Estimate | lwr | upr | |
|---|---|---|---|
| boucherie - laitier | 1.39 | 0.46 | 4.23 |
| cervidé - laitier | 2.25 | 0.77 | 6.61 |
| autre - laitier | 1.36 | 0.23 | 8.00 |
| cervidé - boucherie | 1.62 | 0.50 | 5.22 |
| autre - boucherie | 0.98 | 0.16 | 6.10 |
| autre - cervidé | 0.60 | 0.10 | 3.68 |
Réponse: Non la variable type n’est plus associée à l’incidence de tuberculose.
3.8. Un modèle de régression binomiale négative permettrait peut-être de modéliser correctement cette sur-dispersion. Évaluez un tel modèle. Est-ce que le paramètre de dispersion semble significativement différent de zéro? Effectuez un test de rapport de vraisemblance comparant les modèles de régression binomial négative et de Poisson.
#Le modèle Binomial négatif
modele_nb <- glm.nb(data=tb,
reactors ~ type + offset(log_par)
)
summary(modele_nb)##
## Call:
## glm.nb(formula = reactors ~ type + offset(log_par), data = tb,
## init.theta = 0.4472788933, link = log)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.5695 -0.8400 -0.5043 -0.1769 2.6508
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -8.8516 0.5846 -15.143 <2e-16 ***
## typeboucherie 0.5412 0.6461 0.838 0.402
## typecervidé 0.5163 0.6441 0.801 0.423
## typeautre 0.8685 1.0054 0.864 0.388
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(0.4473) family taken to be 1)
##
## Null deviance: 98.108 on 133 degrees of freedom
## Residual deviance: 97.297 on 130 degrees of freedom
## AIC: 335.44
##
## Number of Fisher Scoring iterations: 1
##
##
## Theta: 0.447
## Std. Err.: 0.107
##
## 2 x log-likelihood: -325.438library(lmtest)
lrtest(modele_incid,
modele_nb)## Likelihood ratio test
##
## Model 1: reactors ~ type + offset(log_par)
## Model 2: reactors ~ type + offset(log_par)
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 4 -259.74
## 2 5 -162.72 1 194.04 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Réponse: Le test de rapport de vraisemblance indique que le modèle Binomial négatif est statistiquement meilleur que le modèle de Poisson (P <0.001).
3.9. Comparez graphiquement le compte d’animaux positifs à la tuberculose prédits par ce dernier modèle et les comptes réels d’animaux positifs. Que notez-vous?
#En premier, nous réunissons les valeurs observées et prédites dans un jeu de données.
obs_pred <- data.frame(cbind(obs=modele_nb$y,
pred=modele_nb$fitted.values)
)
#Ensuite on génère les deux polygones de fréquence dans une même figure.
library(ggplot2)
ggplot(data=obs_pred,
mapping=aes(x=obs)
) +
geom_freqpoly(color="blue")+ #Nous demandons d'abord une ligne pour les valeurs observées
guides(color=FALSE) + #Nous demandons à ne pas avoir de légende dans ce cas
geom_freqpoly(mapping=aes(x=pred,
color="red")
) + #Nous demandons ensuite une ligne pour les valeurs prédites
xlim(0, NA) + #On enlève les valeurs sous zéro
theme_bw() #Un thème blanc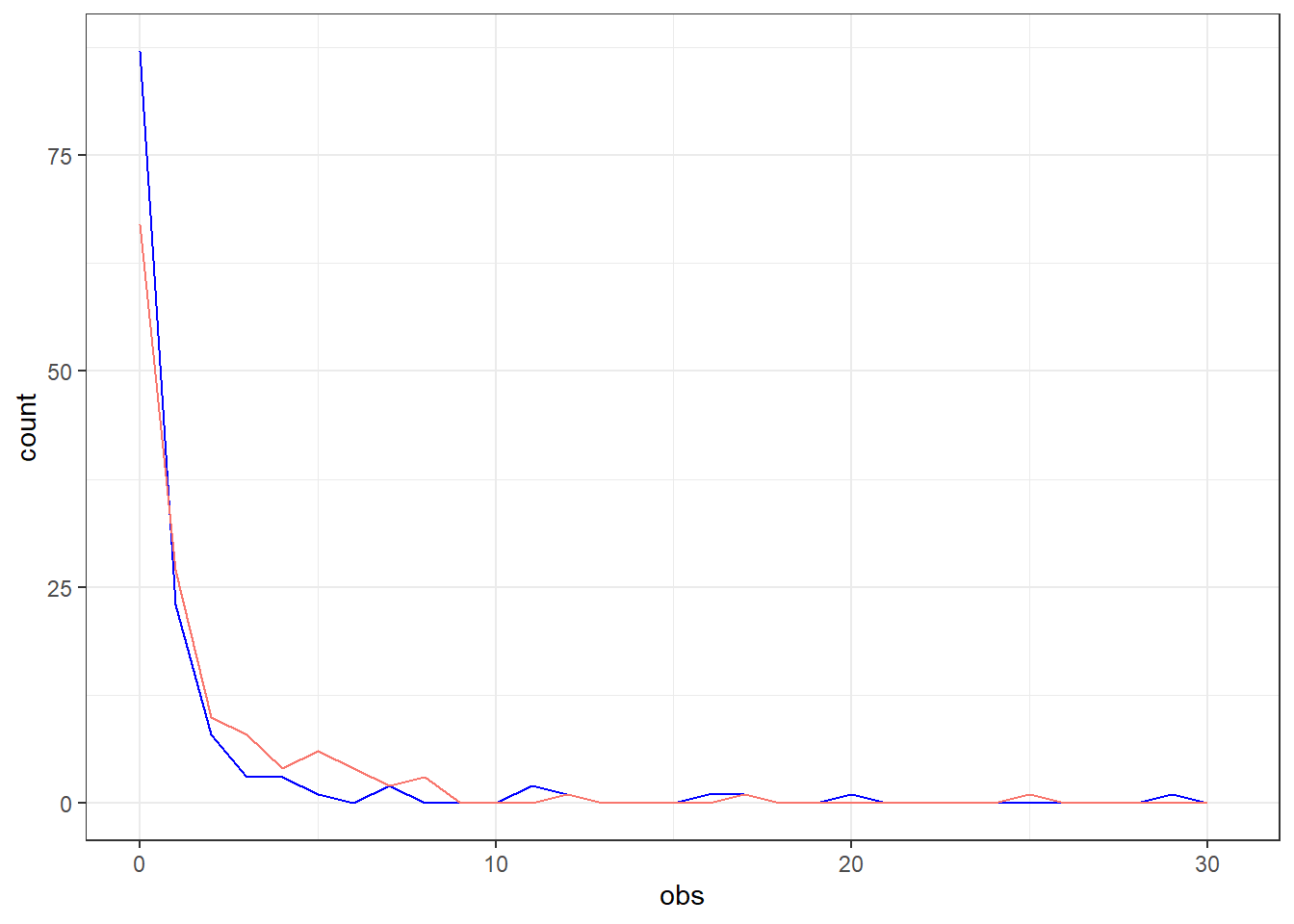
Figure 8.2: Comparaison des comptes d’animaux réactifs observés (bleu) et prédits (rouge).
Réponse: On note que le modèle prédit moins de troupeaux avec près de 0 animal positif (environ 60% des troupeaux) que la réalité (environ 87%). Par contre, le modèle est capable de prédire des comptes assez élevés (jusqu’à 25 animaux réactifs).
8.6 Travaux pratiques 7 - Modèles modifiés en zéro et calcul d’un risque relatif
8.6.1 Exercices
Pour les questions 1 à 3 du TP utilisez le fichier fec.csv (voir description VER p.811).
Dans cette étude nous souhaitons décrire les facteurs de risque associés au compte d’oeufs de parasites dans les fèces de bovins laitiers. La variable fec représente le nombre d’oeufs/5g de fèces qui pourra être prédit en fonction de différents prédicteurs. Dans cet exemple il n’y a pas de dénominateur à considérer (i.e. une variable offset n’est pas nécessaire; chaque animal a été échantillonné une seule fois).
D’abord représenter graphiquement la variable fec. S’agit-il d’une distribution typique pour une donnée de compte? Quelle proportion des observations avait un compte de zéro oeuf?
Essayez d’abord de modéliser l’effet de tx (un traitement à l’Eprinomectin au vêlage) sur le compte d’oeuf (fec) en prenant en compte les facteurs confondants lact, man_heif et man_lact à l’aide d’une régression binomiale négative.
2.1. D’abord, est-ce que le paramètre de dispersion (i.e. le α) est statistiquement différent de zéro? Qu’est-ce que cela vous indique?
2.2. Est-ce que le modèle est adéquat pour vos données?
2.3. Vérifiez si un modèle zéros-enflé Binomial négatif (ZINB) serait préférable à un modèle Binomial négatif.
2.4. À l’aide de ce dernier modèle, expliquez l’effet du traitement à l’Eprinomectin sur le compte d’oeufs de parasite.
Pour la question 3 du TP utilisez le fichier daisy2.csv (voir description VER p.809).
Ne sélectionnez que les 7 troupeaux avec H7=1 et n’utilisez que la 1ère lactation de chaque vache (study_lact=1).
- Dans cette étude on se demande si une rétention placentaire (rp) affecte la probabilité de conception à la première saillie (fs) après avoir contrôlé pour l’âge de la vache (parity). Les chercheurs désirent calculer la fraction attribuable dans la population (AFp).
3.1. Dans ce cas, est-ce que ce serait correct de remplacer le risque relatif dans l’équation précédente par un rapport de cotes estimé à l’aide d’un modèle de régression logistique?
3.2. Quel serait le risque relatif de conception à la 1ère saillie et son IC 95% lorsque rétention placentaire est présent vs. absent et après ajustement pour l’âge de la vache?
3.3. Quelle serait la fraction attribuable (AFp) dans la population due aux rétentions placentaires? Comment interprétez-vous ce résultat?
3.4. Question bonus (i.e. vous aurez 2 banana-points supplémentaires si vous répondez correctement): Comment pourriez-vous obtenir un IC 95% pour l’AFp?
8.6.2 Code R et réponses
Pour les questions 1 à 3 du TP utilisez le fichier fec.csv (voir description VER p.811).
#Nous importons la base de données
fec <-read.csv(file="fec.csv",
header=TRUE,
sep=";")
#On recode certaines variables
fec$fec<-as.numeric(fec$fec)
fec$lact<-as.factor(fec$lact)
fec$past_lact<-as.factor(fec$past_lact)
fec$man_heif<-as.factor(fec$man_heif)
fec$man_lact<-as.factor(fec$man_lact)
#Visualisons la base de données
head(fec)## province herd cow visit tx fec lact season past_lact man_heif man_lact
## 1 1 1 46 5 0 3 1 2 1 0 0
## 2 1 1 46 6 0 3 1 2 1 0 0
## 3 1 1 46 7 0 11 1 2 1 0 0
## 4 1 1 46 8 0 7 1 3 1 0 0
## 5 1 1 46 9 0 17 1 3 1 0 0
## 6 1 1 46 10 0 6 1 3 1 0 0Dans cette étude nous souhaitons décrire les facteurs de risque associés au compte d’oeufs de parasites dans les fèces de bovins laitier. La variable fec représente le nombre d’oeufs/5g de fèces qui pourra être prédit en fonction de différents prédicteurs. Dans cet exemple il n’y a pas de dénominateur à considérer (i.e. une variable offset n’est pas nécessaire; chaque animal a été échantillonné une seule fois).
- D’abord représenter graphiquement la variable fec. S’agit-il d’une distribution typique pour une donnée de compte? Quelle proportion des observations avait un compte de zéro oeuf?
#Distribution de notre variable dépendante (fec)
library(ggplot2)
ggplot(fec,
aes(x=fec)
) +
geom_histogram(colour="black",
fill="grey"
) +
theme_bw() +
xlab("Nombre d'oeufs/5g de fèces") +
ylab("Nombre de vache")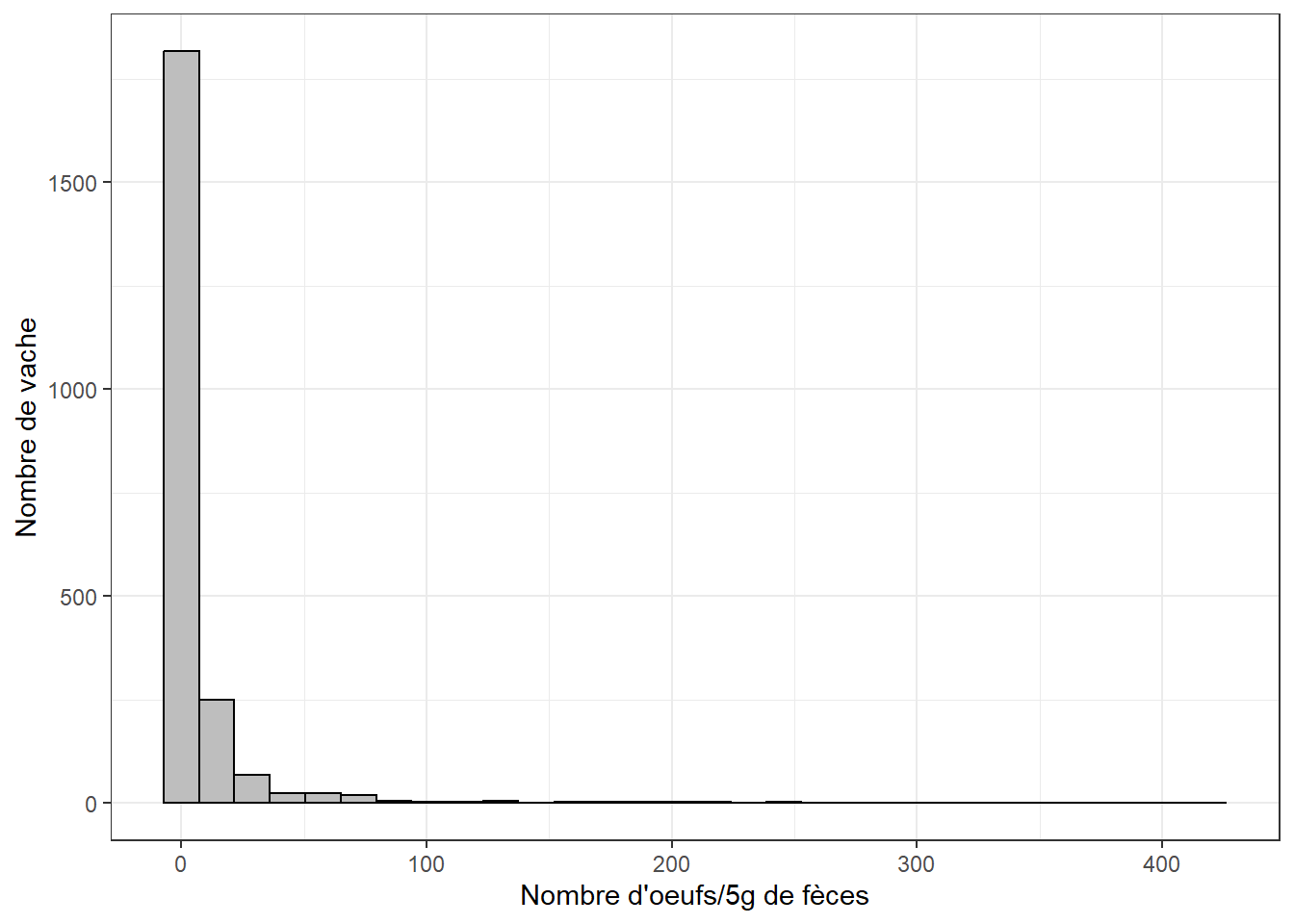
Figure 8.3: Distribution des comptes d’oeufs/5g de fèces.
Réponse: La distribution du compte d’oeufs est « skewed » comme le sont souvent les données de compte et d’incidence. 50% des observations ont un compte de zéro oeuf.
- Essayez d’abord de modéliser l’effet de tx (un traitement à l’Eprinomectin au vêlage) sur le compte d’oeuf (fec) en prenant en compte les facteurs confondants lact, man_heif et man_lact à l’aide d’une régression binomiale négative.
# Le modèle BN
library(MASS)
modele_nb <- glm.nb(data=fec,
fec ~ tx + lact + man_heif + man_lact
)
summary(modele_nb)##
## Call:
## glm.nb(formula = fec ~ tx + lact + man_heif + man_lact, data = fec,
## init.theta = 0.2034616714, link = log)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.5454 -1.1257 -0.8016 -0.1563 5.0501
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.58438 0.08977 28.789 < 2e-16 ***
## tx -0.85893 0.13467 -6.378 0.000000000179 ***
## lact1 -1.10775 0.10696 -10.356 < 2e-16 ***
## man_heif1 -1.26782 0.13150 -9.641 < 2e-16 ***
## man_lact1 1.68948 0.13427 12.583 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(0.2035) family taken to be 1)
##
## Null deviance: 2361.7 on 2249 degrees of freedom
## Residual deviance: 2020.3 on 2245 degrees of freedom
## AIC: 10560
##
## Number of Fisher Scoring iterations: 1
##
##
## Theta: 0.20346
## Std. Err.: 0.00755
##
## 2 x log-likelihood: -10548.111002.1. D’abord, est-ce que le paramètre de dispersion (i.e. le Theta) est statistiquement différent de zéro? Qu’est-ce que cela vous indique?
# Un modèle Poisson
modele_p <- glm(data=fec,
fec ~ tx + lact + man_heif + man_lact,
family="poisson"
)
#Test de rapport de vraisemblance
library(lmtest)
lrtest(modele_p,
modele_nb)## Likelihood ratio test
##
## Model 1: fec ~ tx + lact + man_heif + man_lact
## Model 2: fec ~ tx + lact + man_heif + man_lact
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 5 -30918.0
## 2 6 -5274.1 1 51288 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Réponse: Oui le paramètre de dispersion est statistiquement différent de zéro puisque son IC 95% (0.203 +/- 1.96*0.008) n’inclus pas la valeur zéro. Un test de rapport de vraisemblance comparant des modèles Poisson et Binomial négatif arrive aux mêmes conclusions (P < 0.001). Cela indique que le modèle de régression Binomial négatif est préférable au modèle de Poisson (i.e. la variance n’égale pas la moyenne pour au moins un profil de prédicteurs).
2.2. Est-ce que le modèle est adéquat pour vos données?
library(DHARMa)
#Permet de générer des résiduels par simulation
negbin_simulation <- simulateResiduals(fittedModel = modele_nb)
#Permet de visualiser les résiduels vs les valeurs prédites.
plotSimulatedResiduals(simulationOutput = negbin_simulation)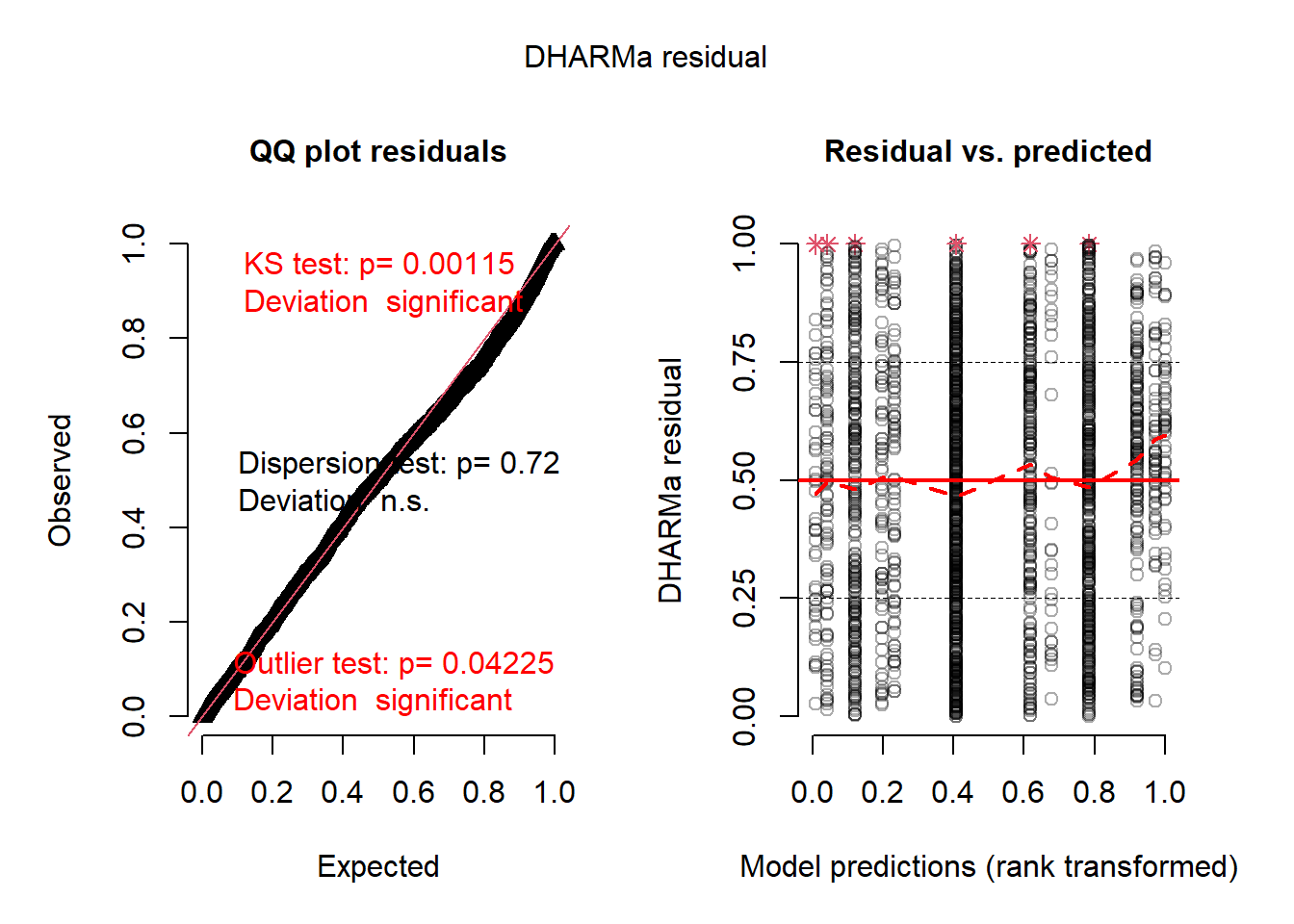
#Permet de tester avec le Pearson chi-square test s'il y a surdispersion
testDispersion(negbin_simulation,
type="PearsonChisq")##
## Parametric dispersion test via mean Pearson-chisq statistic
##
## data: negbin_simulation
## dispersion = 2.21, df = 2245, p-value < 2.2e-16
## alternative hypothesis: two.sidedRéponse: Le test de de Pearson indique que le modèle n’est pas adéquat pour les données (P < 0.05). Donc le modèle ne semble pas adéquat. Sur la figure, il semble y avoir 6 profils de prédicteurs problématiques (sur 12 profils potentiels).
2.3. Vérifiez si un modèle zéros-enflé Binomial négatif (ZINB) serait préférable à un modèle Binomial négatif.
library(pscl)
modele_zinb <- zeroinfl(data=fec,
fec ~ tx + lact + man_heif + man_lact,
dist="negbin"
)
vuong(modele_nb,
modele_zinb)## Vuong Non-Nested Hypothesis Test-Statistic:
## (test-statistic is asymptotically distributed N(0,1) under the
## null that the models are indistinguishible)
## -------------------------------------------------------------
## Vuong z-statistic H_A p-value
## Raw -2.524802 model2 > model1 0.0057882
## AIC-corrected -1.698782 model2 > model1 0.0446801
## BIC-corrected 0.663091 model1 > model2 0.2536362Réponse: En appliquant le test de Vuong, on note que 2 des 3 tests statistiques réalisés suggèrent que le modèle ZINB est supérieur au NB.
2.4. À l’aide de ce dernier modèle, expliquez l’effet du traitement à l’Eprinomectin sur le compte d’oeufs de parasite.
#Ayayaye! ;-)
# LA PARTIE LOGISTIQUE
# Extraire les coefficients et les erreurs types de la partie logistique (binomiale) du modèle dans une même table
coefs_logi <- as.data.frame(summary(modele_zinb)$coefficients$zero[,1:2])
names(coefs_logi)[2] = "SE"
# Calculer les IC95
coefs_logi$lower.ci <- coefs_logi$Estimate-1.96*coefs_logi$SE
coefs_logi$upper.ci <- coefs_logi$Estimate+1.96*coefs_logi$SE
#Ici on pourrait déjà renverser tous les coefficients et les CI
# Mettre à l'exposant les coefficients
OR <- exp(coefs_logi)
# Retirer l'intercept (la 1ère rangée) et les erreurs-types
OR <- OR[-c(1), ]
OR <- subset(OR, select = -c(SE))
# LA PARTIE COMPTE
# Extraire les coefficients et les erreurs types de la partie Binomiale négative du modèle dans une même table
coefs <- as.data.frame(summary(modele_zinb)$coefficients$count[,1:2])
names(coefs)[2] = "SE"
# Calculer les IC95
coefs$lower.ci <- coefs$Estimate-1.96*coefs$SE
coefs$upper.ci <- coefs$Estimate+1.96*coefs$SE
# Mettre à l'exposant les coefficients
IR <- exp(coefs)
# Retirer l'intercept (la 1ère rangée), le paramètre de dispersion (la 6ième rangée) et les erreurs-types
IR <- IR[-c(1, 5), ]
IR <- subset(IR,
select=-c(SE)
)
#Finalement, on pourra demander à voir ces tables
library(knitr)
library(kableExtra)
kable(round(OR,
digits=2),
caption="Partie logistique du modèle zéro-enflé Binomial négatif (ZINB).")%>%
kable_styling()| Estimate | lower.ci | upper.ci | |
|---|---|---|---|
| tx | 1.24 | 0.60 | 2.590000e+00 |
| lact1 | 1.93 | 0.99 | 3.790000e+00 |
| man_heif1 | 1.36 | 0.58 | 3.200000e+00 |
| man_lact1 | 0.00 | 0.00 | 2.116468e+153 |
kable(round(IR,
digits=2),
caption="Partie binomiale négative du modèle zéro-enflé Binomial négatif (ZINB).")%>%
kable_styling()| Estimate | lower.ci | upper.ci | |
|---|---|---|---|
| tx | 0.44 | 0.33 | 0.58 |
| lact1 | 0.38 | 0.31 | 0.47 |
| man_heif1 | 0.29 | 0.22 | 0.38 |
| Log(theta) | 0.26 | 0.23 | 0.29 |
Réponse: Les vaches traitées à l’Eprinomectin au vêlage avaient 1.24 (IC 95% : 0.60, 2.59) fois les odds de ne pas avoir d’oeufs de parasites dans leur fèces comparativement aux vaches non traitées et elles avaient 0.44 (IC 95% : 0.33, 0.58) fois le nombre d’oeufs de parasites des vaches non-traitées.
Pour la question 3 du TP utilisez le fichier daisy2.csv (voir description VER p.809).
daisy2 <- read.csv(file="daisy2.csv",
header=TRUE,
sep=",")Ne sélectionnez que les 7 troupeaux avec H7=1 et n’utilisez que la 1ère lactation observée sur chaque vache (study_lact=1).
daisy2_mod<-subset(daisy2, h7==1)
daisy2_mod<-subset(daisy2_mod,
study_lact==1)- Dans cette étude on se demande si une rétention placentaire (rp) affecte la probabilité de conception à la première saillie (fs) après avoir contrôlé pour l’âge de la vache (parity). Les chercheurs désirent calculer la fraction attribuable dans la population (AFp).
3.1. Dans ce cas, est-ce que ce serait correct de remplacer le risque relatif dans l’équation précédente par un rapport de cotes estimé à l’aide d’un modèle de régression logistique?
library(summarytools)
print(dfSummary(daisy2_mod$fs),
method='render')Data Frame Summary
daisy2_mod
Dimensions: 1795 x 1Duplicates: 1792
| No | Variable | Stats / Values | Freqs (% of Valid) | Graph | Valid | Missing | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | daisy2_mod [integer] |
|
|
1432 (79.8%) | 363 (20.2%) |
Generated by summarytools 1.0.1 (R version 4.2.0)
2023-01-19
Réponse: 50% des observations ont fs=1. Il ne s’agit donc pas d’un événement rare (i.e. < 5%). Ce ne serait pas approprié d’utiliser une supposition qui n’est valide que si la maladie est rare.
3.2. Quel serait le risque relatif de conception à la 1ère saillie et son IC 95% lorsque rétention placentaire est présent vs. absent et après ajustement pour l’âge de la vache?
modele_poisson <- glm(data=daisy2_mod,
fs ~ rp + parity,
family="poisson")
#On demande la variance robuste
library(sandwich)
rob_SE <-sqrt(diag(sandwich(modele_poisson)))
#Pour faciliter la lecture, nous pourrions ajouter les erreurs-types robustes à mes coefficients dans une table
tab_SE <- data.frame(cbind(Estimate=modele_poisson$coefficients,
robust_SE=rob_SE)
)
#Puis calculer les IC95
tab_SE$lower.ci <- tab_SE$Estimate-1.96*tab_SE$robust_SE
tab_SE$upper.ci <- tab_SE$Estimate+1.96*tab_SE$robust_SE
#Enlever l'intercept, les SE et mettre tout à l'exposant pour avoir des RR
tab_SE <- tab_SE[-c(1), ]
tab_SE <- exp(subset(tab_SE,
select=-c(robust_SE)
)
)
library(knitr)
library(kableExtra)
kable(round(tab_SE,
digits=2),
caption="Modèle de Poisson avec erreurs-types robustes pour estimer le risque relatif de conception à la 1ère saillie.")%>%
kable_styling()| Estimate | lower.ci | upper.ci | |
|---|---|---|---|
| rp | 0.91 | 0.75 | 1.09 |
| parity | 0.95 | 0.92 | 0.99 |
Réponse: Le risque de conception à la première saillie pour une vache qui a eu une rétention placentaire était 0.91 fois (IC 95% : 0.75, 1.09) celui d’une vache qui n’a pas eu de rétention placentaire. Ce n’est pas statistiquement significatif cependant.
3.3. Quelle serait la fraction attribuable (AFp) dans la population due aux rétentions placentaires? Comment interprétez-vous ce résultat?
#Vérifier prévalence de l'exposition (rp)
library(summarytools)
print(dfSummary(daisy2_mod$rp),
method='render')Data Frame Summary
daisy2_mod
Dimensions: 1795 x 1Duplicates: 1793
| No | Variable | Stats / Values | Freqs (% of Valid) | Graph | Valid | Missing | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | daisy2_mod [integer] |
|
|
1795 (100.0%) | 0 (0.0%) |
Generated by summarytools 1.0.1 (R version 4.2.0)
2023-01-19
#Calculer l'AFp
afp <- 0.101*(0.91-1)/(0.101*(0.91-1)+1)
afp## [1] -0.009173386Réponse: En supposant que la relation est causale, une réduction de 1% (i.e., -0.009) de la conception à la 1ère saillie serait due aux rétentions placentaires.
3.4. Question bonus (i.e. vous aurez 2 banana-points supplémentaires si vous répondez correctement): Comment pourriez-vous obtenir un IC 95% pour l’AFp?
Réponse: À l’aide du Bootstrap, on pourrait recréer un grand nombre de jeux de données et estimer le risque relatif et la prévalence de rétention placentaire dans chaque jeu de données. Ensuite, on calcule l’AFp de chaque jeu de données et on rapporte le percentile 2.5 et 97.5 de l’AFp comme IC 95%.